WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Constructies van vijfhoek en zeshoek

Dit is een reactie op vraag 89592

Beste, Dankjewel voor het uitleg.

Ik heb nog een vraagje:

Ik heb het manier ook voor zeshoek geprobeerd, maar lukte mij niet om x en y uit te drukken door de volgende middelpunten die ik zelf gekozen heb:

M1(2,4); M2(5,2); M3(10,2); M4(12,5); M5(10,4); M6(5,6).

Ik krijg aan het eind: x = x en y = 6-y... En dat kan niet. Waar heb ik hier fout gemaakt?

Hier zijn mijn gevonden coördinaten voor P1P2P3P4P5P6:

Voor P1 (x,y)
Voor P2(4-x,8-y)
Voor P3(6+x,-4+y)
Voor P4(14-x,8-y)
Voor P5(10+x,2+y)
Voor P6(10-x,6-y)

Er is hier een fout opgetreden, maar ik zie die fout niet. Graag jouw hulp daarover. Alvast bedankt.
M
Student hbo - dinsdag 14 april 2020

Antwoord

Bij een zeshoek werkt dat dus niet! Bij 6 gegeven middelpunten valt er kennelijk weinig meer te kiezen! Hoe zit dat? Hoe komt dat? Waarom is dat? Genoeg vragen om te onderzoeken.

Naschrift

Je kunt G'' (het eindpunt) wel op P (het begigpunt) krijgen door één van de gegeven middelpunten te verplaatsen.

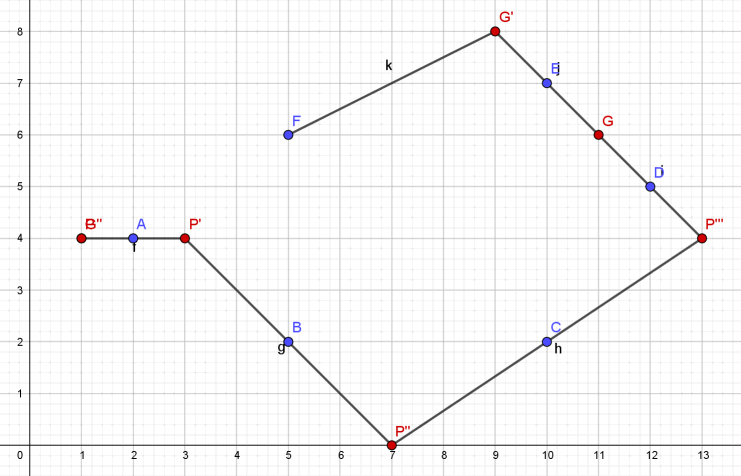
Ik heb E(10,4) verplaatst naar E{10,7). Dan lukt het wel...

Bij de vijfhoek kreeg je voor de x-coördinaat steeds x, -x, x, -x, ... Om dat het oneven is houd je altijd een x over. Bij de zeshoek ben je alle x-en kwijt. Idem voor de y-coördinaat.

Het lag dus niet aan jou!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 14 april 2020

Re: Re: Re: Constructies van vijfhoek en zeshoek