|
|
|
\require{AMSmath}
Re: Re: Re: Constructies van vijfhoek en zeshoek
Dus er is een iets aan de hand als n (n-hoek) oneven en n even is. Hoe zullen we dat formuleren?
Hier komen bepaalde vragen aan de boord die ik nog niet begrijp.- Als wij veralgemeniseren: als er een n-hoek bestaat, hoe vinden we die dan?
Dus hoe kunnen we bijvoorbeeld P1 synthetisch vinden, gegeven M1, M2, M3, ..., Mn? - En hoe hangt P1 algebraïsch af van M1, M2, M3, ..., Mn?
- Of is P1 misschien vrij te kiezen (en voldoen er dus oneindig veel n-hoeken)?
Tot heden zie ik het nog niet. Graag jouw hulp daarvan. Alvast bedankt.
De groeten van M.
M
Student hbo - dinsdag 14 april 2020
Antwoord
n is oneven
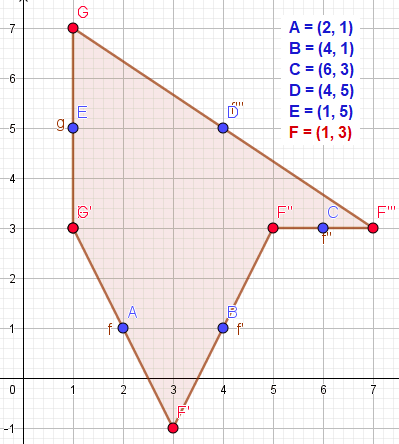
Bij een oneven aantal middelpunten kan je een mogelijk beginpunt berekenen door de $x$ en $y$ om en om op te tellen en af te trekken. Hier bestaat een $P_1$, maar je kunt dat niet vrij kiezen.
Voorbeeld
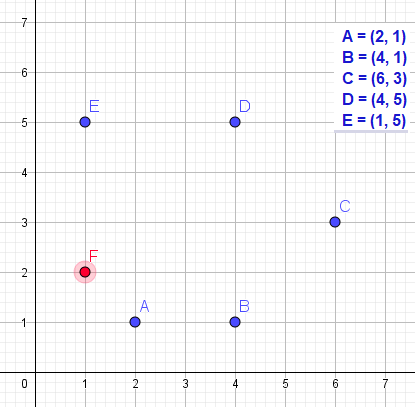
x = 2 - 4 + 6 - 4 + 1 = 1
y = 1 - 1 + 3 - 5 + 5 = 3
Dat punt $P_1$ moet dan (1,3) zijn.
n is even
Ik vermoed dat bij een even aantal middelpunten die een zeshoek opleveren moet gelden dat de x en y bij optellen/aftrekking beide uitkomen op nul. Er is dus niet altijd een mogelijk beginpunt.
Voorbeeld
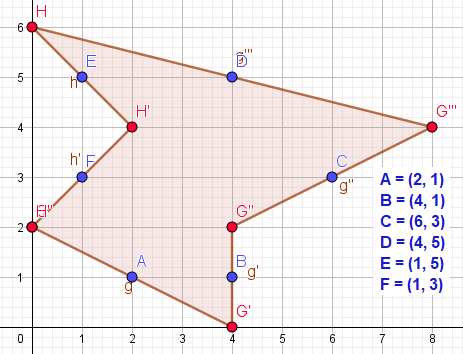
x = 2 - 4 + 6 - 4 + 1 - 1 = 0
y = 1 - 1 + 3 - 5 + 5 - 3 = 0
Maar dat laatste moet je dan nog aantonen!
Nu jij weer!
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 14 april 2020
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 89605