WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Onderlinge ligging van rechten en vlakken

Toon aan dat de middens M, N, P en Q van de ribben AB, BC, CD, DA van een viervlak ABCD in eenzelfde vlak liggen en een parallellogram vormen.
De Roc
2de graad ASO - zondag 23 maart 2003

Antwoord

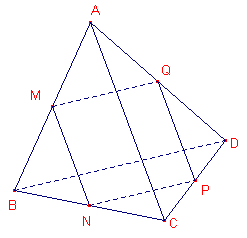
Tja, het bewijs hangt een beetje af van welke stellingen en definities er (eerder) zijn gegeven.

In ieder geval bepalen de lijn MN en het punt Q een vlak V.
In driehoek ABC is MN middenparallel, zodat MN // AC
In driehoek ACD is PQ middenparallel, zodat PQ // AC
Hieruit volgt dat MN // PQ
De lijn QP ligt nu ook in het vlak V.
Omdat MQ twee punten met V gemeen heeft ligt MQ geheel in vlak V.
Evenzo geldt dat voor NP.
En ook NP // BD en MQ // BD waaruit volgt dat NP // MQ.
En dan is MNPQ een parallellogram.
- Kijk zelf nog eens welke stellingen (definities en wellicht axioma's) moeten worden gebruikt om tot het bovenstaande te komen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 23 maart 2003