WisFaq!

Onderlinge ligging van rechten en vlakken

Toon aan dat de middens M, N, P en Q van de ribben AB, BC, CD, DA van een viervlak ABCD in eenzelfde vlak liggen en een parallellogram vormen.

De Rocker Melanie
23-3-2003

Antwoord

Tja, het bewijs hangt een beetje af van welke stellingen en definities er (eerder) zijn gegeven.

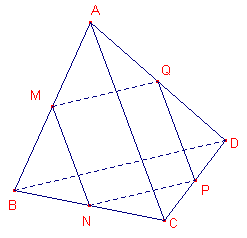
In ieder geval bepalen de lijn MN en het punt Q een vlak V.
In driehoek ABC is MN middenparallel, zodat MN // AC
In driehoek ACD is PQ middenparallel, zodat PQ // AC
Hieruit volgt dat MN // PQ
De lijn QP ligt nu ook in het vlak V.
Omdat MQ twee punten met V gemeen heeft ligt MQ geheel in vlak V.
Evenzo geldt dat voor NP.
En ook NP // BD en MQ // BD waaruit volgt dat NP // MQ.
En dan is MNPQ een parallellogram.
- Kijk zelf nog eens welke stellingen (definities en wellicht axioma's) moeten worden gebruikt om tot het bovenstaande te komen.

dk
23-3-2003