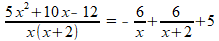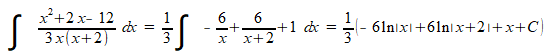WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Breuksplitsing?

Dit is een reactie op vraag 88324

Goede morgen Gilbert,

De toevoeging van de derde term C/1 in de splitsingsformule van de breuk begrijp ik niet.
Na substitutie van de voor A en B gevonden waarden van - 6 respectievelijk + 6 blijkt de waarde van C inderdaad 1(één) te zijn terwijl je daar nou juist de waarde 0(nul) zou verwachten.
De waarde 1 is vervolgens ook in de integraalformule opgenomen.
Heeft dit nog gevolgen voor het primitiveren ervan? Je zou 'm bijv. kunnen mee-integreren tot "x" waarvan de afgeleide toch ook altijd gelijk aan 1 is.
Adriaa
Ouder - donderdag 1 augustus 2019

Antwoord

Hallo Adriaan,

Waarom zou je de waarde C=0 verwachten? Probeer de breuk maar eens te splitsen zonder de term C. Je zult ontdekken dat je de coëfficiënt voor x² niet correct kunt krijgen. Ik verwacht dus juist niet C=0.

Wellicht ben je verbaasd dat we voor C de 'neutrale' waarde 1 vinden, maar dit is toeval. Splits zelf als voorbeeld maar eens de volgende breuk van eenzelfde vorm maar met wat andere getallen, je vindt C=5:

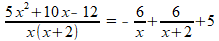
Uiteraard moet je de waarde van C mee-integreren. Na breuksplitsen blijkt de oorspronkelijke breuk gelijk te zijn aan de som van drie termen. De intergraal van de oorspronkelijke breuk is dan ook de integraal van het totaal van deze drie termen, niet de integraal van een willekeurig gedeelte van deze drie termen. Je vindt dus:

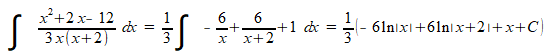
Meer informatie vind je op breuksplitsen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 1 augustus 2019