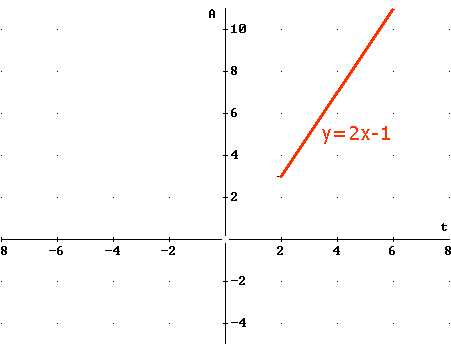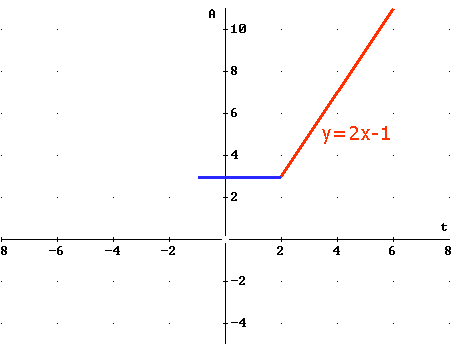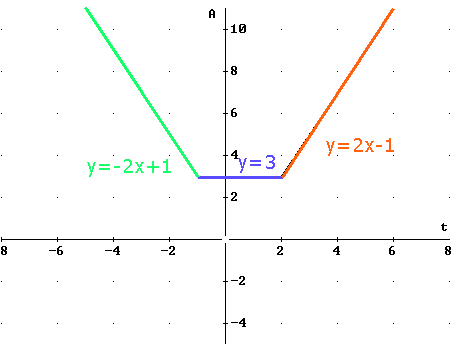|
|
|
\require{AMSmath}



Re: Grafiek modulusfunctie
Ja,
x$>$2 en x$>$-1
x$>$2 en x$<$-1
x$<$2 en x$>$-1
x$<$2 en x$<$-1
Maar nu?
Mboudd
Leerling mbo - zondag 28 oktober 2018
Antwoord
Teken de grafiek van $f(x)=|x-2|+|x+1|$
Dat gaat zo:
I.
Bij $x-2\ge0$ en $x+1\ge0$ gaat de formule over in:
$f(x)=x-2+x+1=2x-1$ voor $x\ge2$.
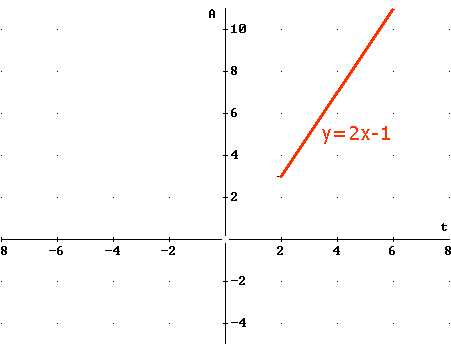
II.
Bij $x-2\ge0$ en $x+1<0$ gaat de formule over in:
$f(x)=x-2-x-1=-3$ voor $x\ge2$ en $x<-1$. Dat kan niet.
III.
Bij $x-2<0$ en $x+1\ge0$ gaat de formule over in:
$f(x)=-x+2+x+1=3$ voor $x<2$ en $x\ge-1$.
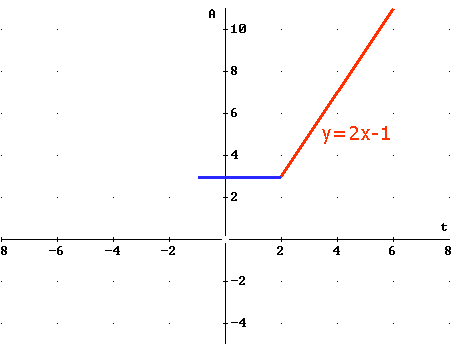
IV.
Bij $x-2<0$ en $x+1<0$ gaat de formule over in:
$f(x)=-x+2-x-1=-2x+1$ voor $x<-1$.
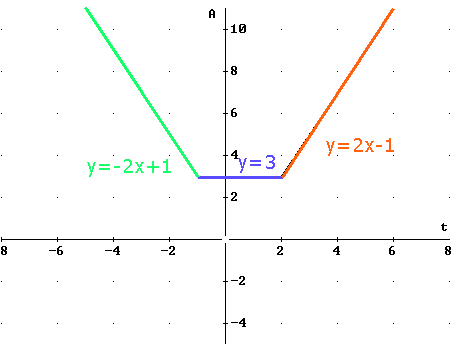
Je vertaalt de voorwaarden naar een nieuw functievoorschrift zonder absoluutstrepen en je bepaalt voor welk interval de nieuwe formule geldt.
Helpt dat?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 28 oktober 2018
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 87005
Dit is een reactie op vraag 87005