WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Snijpunten van twee cirkels

Dit is een reactie op vraag 86827

Uit de vergelijking 2x+2y=25 leid ik af: y=25/2-x. Als ik y inbreng in de formule x²+y²=25 loop ik vast - wat doe ik verkeerd? metdank!
walter
Ouder - woensdag 12 september 2018

Antwoord

Je doet niks fout.

$
\eqalign{
& x^2 + \left( {\frac{{25}}
{2} - x} \right)^2 = 25 \cr
& x^2 + x^2 - 25x + \frac{{625}}
{4} = 25 \cr
& 2x^2 - 25x + \frac{{625}}
{4} = 25 \cr
& 8x^2 - 100x + 625 = 100 \cr
& 8x^2 - 100x + 525 = 0 \cr
& D = \left( { - 100} \right)^2 - 4 \cdot 8 \cdot 525 = - 6800 \cr
& {\text{Geen}}\,\,{\text{oplossing}} \cr}
$

Er zijn geen snijpunten!

Naschrift
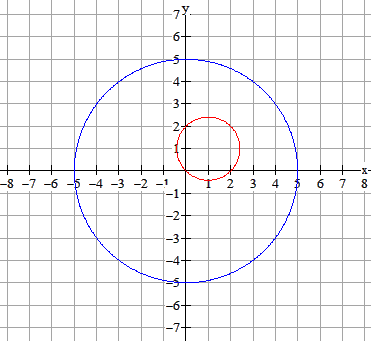
De methode klopt natuurlijk wel, maar 't was wellicht handiger geweest om van tevoren een plaatje te maken:

$
\eqalign{
& x^2 + y^2 = 25 \cr
& x^2 + y^2 - 2x - 2y = 0 \cr
& \cr
& x^2 + y^2 = 25 \cr
& \left( {x - 1} \right)^2 - 1 + \left( {y - 1} \right)^2 - 1 = 0 \cr
& \cr
& x^2 + y^2 = 25 \cr
& \left( {x - 1} \right)^2 + \left( {y - 1} \right)^2 = 2 \cr}
$

Zie ook cirkelvergelijkingen

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 12 september 2018