WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Meetkundige plaats voetpunt loodlijn

Vooraf schets ik even de opgave: Gegeven is een driehoek ABC met een vaste basis BC en A variabel, maar zodanig dat AB+AC = s (constante).

Uit C tekent men de loodlijn op de buitendeellijn m van de hoek A. Noem P het voetpunt van die loodlijn op m. Bepaal de meetkundige plaats van het voetpunt P.

Vooreerst maakte ik een tekening (zie bijlage). Het is meteen duidelijk dat wegens AB+AC = s, het punt A beweegt op een ellips (E), met brandpunten B en C, én, gaande door de punten D en E. Noem x de afstand van B tot D resp. C tot E. Om x te bepalen drukt men uit dat x + d +x = s, met d de afstand tussen de brandpunten B en C. Hieruit volgt dat x = (s - d)/2.

Het is ook direct duidelijk dat het hoekpunt A onder BC kan liggen; daar werd A vervangen door A' en P door P' (zie figuur; spiegeling!).

De buitendeellijn van het hoekpunt A, is tezelfdertijd raaklijn aan (E), als B en C brandpunten zijn van (E).

Bij constructie is de hoek(APC) = 90°. Empirisch stelde ik vast dat de hoek(APD) = hoek(CPE), onverschillig de posiitie van A op (E). De hoekwaarde verandert wel, maar de hoeken blijken wel steeds aan elkaar gelijk te zijn.

Voer dan een rotatie van de hoek(APC) = 90° rond het punt P, over een hoek hoek(APD) = hoek(CPE). Dit heeft tot gevolg dat de lijn AP,resp. CP omgezet wordt in de lijn DP resp. EP.

Wegens de gelijkheid hoek(APD) = hoek(CPE), betekent dit dat de hoek(DPE) = 90°, want langs de ene kant wordt de gegeven rechte hoek hoek(APC) verminderd wordt met hoek(APD) en anderzijds met de hoek(CPE) vermeerderd.

Dat betekent dan op zijn beurt dat het voetpunt P op een cirkel (K) moet liggen met middellijn DE.

Het omgekeerde, nl. aantonen dat een willekeurig punt S gelegen op (K) leidt tot de conclusie dat S een voetpunt is van een loodlijn uit C op de buitenraaklijn van het corresponderend hoekpunt A, voorgesteeld door A", stelde geen probleem.

Mijn VRAAG: Hoe kan ik er achteraf in slagen om wiskundig aan te tonen dat hoek(APD) = hoek(CPE). Graag een tip a.u.b. waarmee ik de gelijkheid van die 2 hoeken kan aantonen. Van harte bedankt!
Yves D
Iets anders - maandag 3 september 2018

Antwoord

Beste Yves,

Ik heb het weer eens anders aangepakt, met een eigen plaatje.

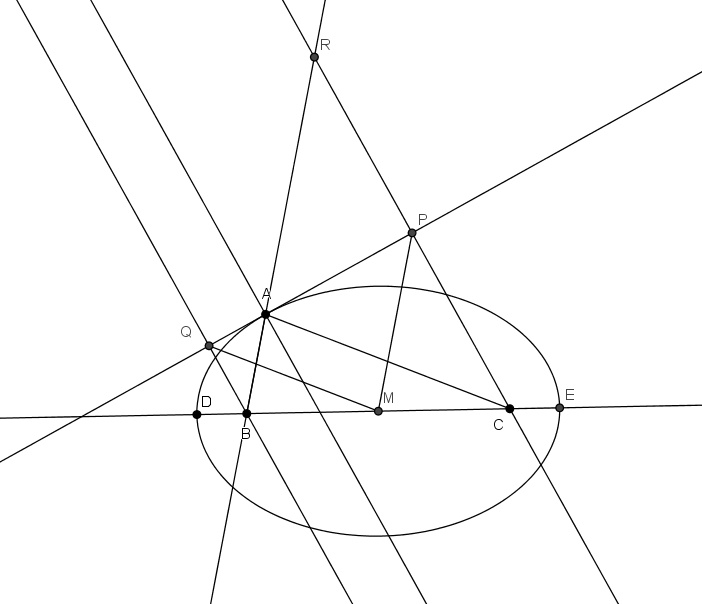
Behalve het punt $P$ op de buitenddeellijn, heb ik ook het voetpunt $Q$ van $B$ de buitendeellijn genomen. $R$ is het snijpunt van $AB$ en $PC$.

Merk nu op dat $\Delta APR \cong \Delta APC$. Nu kun je zien dat $BR = BA+AC = DE = 2ME$.

Bovendien is $P$ het midden van $CR$, zodat $MP // BR$ en $MP = \frac 12 BR = ME$.

$Q$ heb ik achteraf niet nodig gehad.

Met vriendelijke groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 8 september 2018