 |
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
|||||||||||||||||
|
\require{AMSmath}



Verhouding gearceerde oppervlakte tot totale oppervlakte van vijfhoek
AntwoordDe hele vijfhoek bestaat uit 5 gelijke driehoeken MAB, MBC, MCD, MDE en MEA. Het lijnstuk MB verdeelt het gearceerde gebied in twee delen: driehoek MBP en driehoek MBN. Als we de oppervlakten van MBP en MBN uit kunnen drukken in de oppervlakte van MBA resp. MBC zijn we er.



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2025 WisFaq - versie 3 | |||||||||||||||||

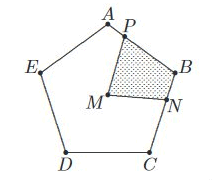 ABCDE is een regelmatige vijfhoek met middelpunt M
ABCDE is een regelmatige vijfhoek met middelpunt M
