WisFaq!

Verhouding gearceerde oppervlakte tot totale oppervlakte van vijfhoek

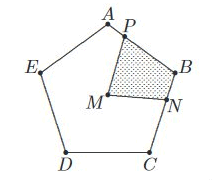
ABCDE is een regelmatige vijfhoek met middelpunt M
waarbij:
|AP| = $\frac{1}{4}$|AB| en |BN| = $\frac{1}{3}$|BC|.

• Wat is de verhouding van de gearceerde oppervlakte tot de totale oppervlakte van de vijfhoek?

JWO 2007 Tweede ronde, Probleem 23 Vlaamse Wiskunde Olympiade

Ik snap er niks van...

Manu
22-2-2018

Antwoord

De hele vijfhoek bestaat uit 5 gelijke driehoeken MAB, MBC, MCD, MDE en MEA. Het lijnstuk MB verdeelt het gearceerde gebied in twee delen: driehoek MBP en driehoek MBN. Als we de oppervlakten van MBP en MBN uit kunnen drukken in de oppervlakte van MBA resp. MBC zijn we er.

Omdat |BN| 1/3 is van |BC| geldt dat de oppervlakte van MBN 1/3 deel is van de oppervlakte van MBC. Snap je dat?

Omdat |AP| 1/4 is van |AB| is |BP| 3/4 deel van |AB|.
Dus is de oppervlakte van MBP ... deel van MBA.

Samen zijn MBP en MBN dus ...+1/3 van MBA.
Dus MBP en MBN samen zijn (...+1/3) van 1/5 van de vijfhoek.
Dus het gearceerde deel is (...+1/3)×1/5 van de vijfhoek en dat is ... deel.

hk
22-2-2018