|
|
|
\require{AMSmath}
Re: Domein bepalen van logaritmische functies
Hoezo x2-5x+6$>$0?
Als ik correct ben kan het domein van een logaritme niet 0 zijn. De vergelijking is als volg:
x2-5x+6$>$1.
Als je uw manier zou toepassen op het volgende:
f(x)=3log(x-1) en je stelt de verglijking x-1$>$0 krijg je 1 waardoor er 1-1=0 ontstaat. Wanneer dit wordt ingevuld in de rekenmachine geeft dit een math error.
Wat hier wordt gegeven is het minimum voor een positieve wortel.
log(x) = x$>$1.
Matthi
Student universiteit - donderdag 14 december 2017
Antwoord
Het domein voor de standaardfunctie is $x\gt0$:
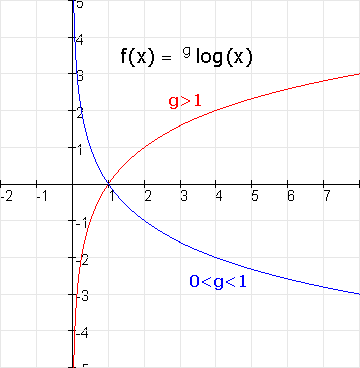
In jouw geval geldt $x-1\gt0$, dus $x\gt1$. Je moet dan niet $x=1$ nemen want dan is de logaritme nu juist niet gedefinieerd. Maar $1,0000000001$ zou best kunnen...
Dus ik denk dat mijn antwoord wel in orde was.
Wat jij allemaal schrijft lijkt me niet in orde. Wat is nu precies het probleem?
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 15 december 2017
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 62844