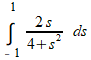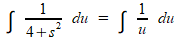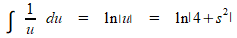WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Substitutiemethode

Hallo,

Bij de volgende integraal blijf ik maar verkeerd uitkomen. Ziet u waar het fout gaat in mijn uitwerking? Ik zou uit moeten komen op 0

getal voor het integraalteken is de ondergrens, erna is de bovengrens

-1 $\int{}$ 1 ^2s/_4+s²

u(s) = 4+x²
u'(s) = 2s
du/ds = 2s $\to$ du=2sds

invullen geeft:
-1 $\int{}$ 1 ^du/_u
-1 $\int{}$ 1 ¹/_4+s²du
F(s) = ln(4+s²)
F(b) - F(a) = ?
F(1) - (F-1) = 1,609 - 1,098 = 0,510 (maar ik moet op 0 uitkomen)
Bo
Student universiteit - donderdag 14 december 2017

Antwoord

Hallo Bo,

Het gaat om de volgende integraal:

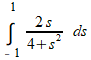
Je aanpak gaat goed tot en met du = 2s·ds

Echter, nu moet je in je oorspronkelijke functie zorgvuldig 2s·ds vervangen door du. In de noemer blijft 4+s² dus wel staan! Je krijgt:

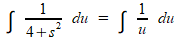
Het is dus opnieuw zaak om zorgvuldig te noteren.

Let ook op de integratiegrenzen: in je oorspronkelijke integraal 'loopt' s van -1 tot 1. Maar nu ga je over u integreren, hier horen andere grenzen bij. Je kunt deze grenzen wel uitrekenen door u te berekenen bij s=-1 en s=1, maar dit is niet nodig. Laat de grenzen in dit stadium maar weg.

Na integratie en terug-substitueren krijg je:

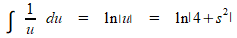
Na deze terug-substitutie ben je terug bij s, dus nu kan je de integraal berekenen door de grenzen in te vullen:

Integraal = F(1) - F(-1)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 14 december 2017