|
|
|
\require{AMSmath}
Re: Newton-Raphson
Ik heb de applet geprobeerd, maar ten eerste krijg ik de grafiek niet goed geplot en begrijp ik ook niet helemaal, wat voor divergerends ik moet zien?
Shahna
Leerling bovenbouw havo-vwo - donderdag 13 maart 2003
Antwoord
OK doen we het anders. We zoeken nulpunten van een functie met Newton-Raphson:
De werkwijze: kies startwaarde x0,
de volgende benadering wordt: xn+1=xn-(f(xn))/(f'(xn))
Nu nemen we de functie f(x) = 1/x2-1/x. Deze functie heeft alleen een nulpunt bij x=1. De vraag is of Newton Raphson dat nulpunt ook altijd vindt.
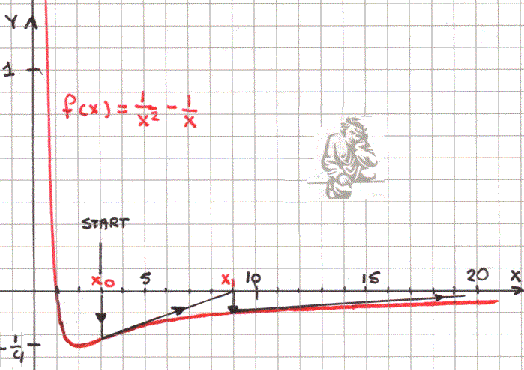
Als gaat rekenen dan zal de recursieformule: xn+1=xn-(f(xn))/(f'(xn))
opleveren xn+1=(2xn2 - 3xn)/(xn - 2).
Startwaarde x0=3 levert dan op x1= 9, x2=19,3 enzovoort.
Dit gaat niet naar het (enige) nulpunt toe. Divergent dus.
Het kan nog veel enger !! Neem f(x)= -3/4x4+13/4x2
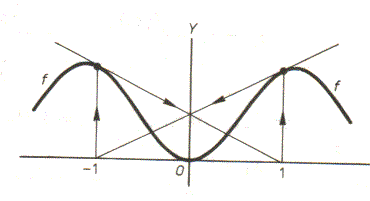
Als gaat rekenen dan zal de recursieformule: xn+1=xn-(f(xn))/(f'(xn))
opleveren xn+1=(7xn - 9xn3)/(14-12xn12).
Kies nu startwaarde x0=1 dan x1=-1 en x2=1 en x3=-1......
Het harmonicaeffect!! Komt dus ook nooit in de buurt van een van de (drie) nulpunten. Daarom wederom divergent.
Met vriendelijke groet
JaDeX
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 14 maart 2003
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 8442