WisFaq!

Re: Newton-Raphson

Ik heb de applet geprobeerd, maar ten eerste krijg ik de grafiek niet goed geplot en begrijp ik ook niet helemaal, wat voor divergerends ik moet zien?

Shahna
13-3-2003

Antwoord

OK doen we het anders. We zoeken nulpunten van een functie met Newton-Raphson:

De werkwijze: kies startwaarde x₀,
de volgende benadering wordt: x_n+1=x_n-(f(x_n))/(f'(x_n))

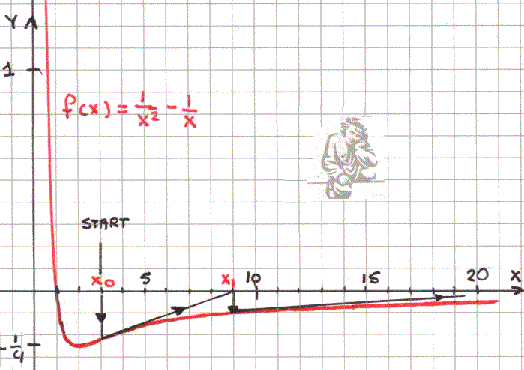
Nu nemen we de functie f(x) = 1/x²-1/x. Deze functie heeft alleen een nulpunt bij x=1. De vraag is of Newton Raphson dat nulpunt ook altijd vindt.



Als gaat rekenen dan zal de recursieformule: x_n+1=x_n-(f(x_n))/(f'(x_n))
opleveren x_n+1=(2x_n² - 3x_n)/(x_n - 2).
Startwaarde x₀=3 levert dan op x₁= 9, x₂=19,3 enzovoort.
Dit gaat niet naar het (enige) nulpunt toe. Divergent dus.

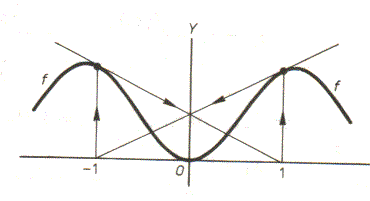
Het kan nog veel enger !! Neem f(x)= -³/₄x⁴+1³/₄x²



Als gaat rekenen dan zal de recursieformule: x_n+1=x_n-(f(x_n))/(f'(x_n))
opleveren x_n+1=(7x_n - 9x_n³)/(14-12x_n¹²).
Kies nu startwaarde x₀=1 dan x₁=-1 en x₂=1 en x₃=-1......
Het harmonicaeffect!! Komt dus ook nooit in de buurt van een van de (drie) nulpunten. Daarom wederom divergent.

Met vriendelijke groet

JaDeX

jadex
14-3-2003