WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

De grootte van een scherpe hoek berekenen

Beste meneer/mevrouw

Alvast bedankt voor het antwoorden.

Ik heb een vraag over mijn extra oefening die ik zou moeten kunnen maken voor het examen. Het gaat als volgt:

Bereken de grootte van een scherpe hoek van B'D met elk van de zijvlakken door D.

Dan krijg je ook nog de bijbehorende informatie over de kubus(de lengtes). Helaas kan ik geen foto toevoegen anders had ik dat zeker gedaan. Zou het mogelijk zijn om te vertellen welke stappen ik zou moet uitvoeren om het maximum op deze vraag te halen? De leerkracht heeft me een beetje op weg geholpen. Misschien dat het voor u ook handig is. Een van de stappen die ik moet uitvoeren is het diagonaal van het voorvlak berekenen. Dat is gedaan met behulp van Pythagoras. Eenmaal als je dat hebt kun je de hoek terugzoeken met behulp van je rekenmachine. (in dit geval de tangens)

Het zou echt veel voor me betekenen als jullie me het konden proberen uit te leggen. Ik kom er namelijk niet uit.

Groetjes

jan
2de graad ASO - zaterdag 20 mei 2017

Antwoord

Hallo Jan,

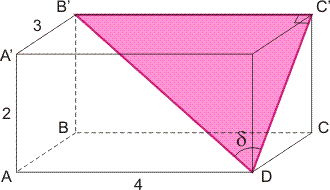
In onderstaande figuur is de balk (geen kubus) getekend, met daarin de lichaamsdiagonaal B'D. Gevraagd is o.a. de hoek tussen deze lichaamsdiagonaal en het voorvlak. Deze hoek heb ik aangegeven met $\delta$:

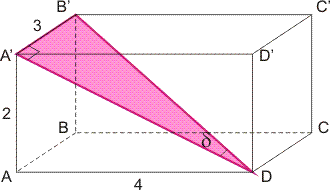
Deze hoek $\delta$ is een hoek van de gekleurde rechthoekige driehoek A'DB'in de balk. Hieronder heb ik deze driehoek getekend zoals je er recht op kijkt:

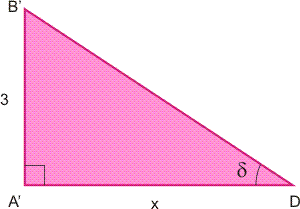
Ga voor jezelf na dat de hoekpunten in de beide figuren overeen komen.
Driehoek A'DB' is rechthoekig. De tangens van hoek D (dus tan$\delta$) is dan 3/x. Wanneer je x (=de aanliggende rechthoekszijde A'D van hoek D) zou weten, dan weet je de tangens van hoek D en kan je hoek D zelf bepalen.

Nu is A'D de diagonaal van het voorvlak van je balk. Dit voorvlak heb ik hieronder nogmaals getekend:

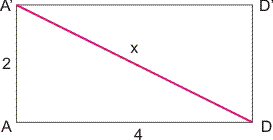
De lengte x van deze diagonaal kan je berekenen met Pythagoras:

x² = 4²+ 2²
x² = 20
x = √20 = √(4·5) = √4√5
x = 2√5

In de tweede figuur zien we nu:

tan$\delta$ = ³/_2√5

Met je rekenmachine bereken je dan:

$\delta\approx$33,9°

Je moet ook de hoeken tussen de lichaamsdiagonaal B'D en de twee andere zijvlakken door D berekenen. Dit gaat op dezelfde manier. In de figuur hieronder zie je de hoek $\delta$ tussen B'D en het ondervlak:

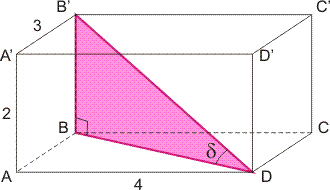
Als tussenstap moet je de diagonaal BD berekenen.

Voor de hoek tussen B'D en het rechter zijvlak gebruik je de driehoek B'DC', je berekent als tussenstap de diagonaal DC':

Lukt het hiermee?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 mei 2017