WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Maximale inhoud van een cilinder bij gegeven oppervlakte

Beste
Ik weet maar niet hoe ik deze oefening kan oplossen. Zou u me kunnen helpen?

Vraag: de oppervlakte van een cilinder is 1 m², bepaal de straal van het grondvlak en de hoogte van de cilinder zodat de inhoud van de cilinder maximaal is.

Heel erg hard bedankt voor uw hulp!
Yente
3de graad ASO - zaterdag 17 september 2016

Antwoord

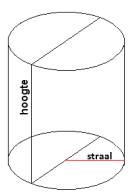Je hebt de volgende formules nodig:

$\eqalign{
& {O_{cilinder}} = 2\pi {r^2} + 2\pi rh \cr
& {I_{cilinder}} = \pi {r^2}h \cr} $

Je weet dat de oppervlakte gelijk is aan 1 m². Dat geeft:

$2\pi {r^2} + 2\pi rh = 1$

Je kunt daarmee $h$ uitdrukken in $r$. Als je dan in de formule voor de inhoud de $h$ vervangt door je uitdrukking in $r$ dan heb je de inhoud uitgedrukt in $r$. Met de afgeleide kan je dan de waarde van $r$ bepalen voor de grootste oppervlakte.

Zou dat lukken?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 17 september 2016

Re: Maximale inhoud van een cilinder bij gegeven oppervlakte