WisFaq!

Maximale inhoud van een cilinder bij gegeven oppervlakte

Beste
Ik weet maar niet hoe ik deze oefening kan oplossen. Zou u me kunnen helpen?

Vraag: de oppervlakte van een cilinder is 1 m², bepaal de straal van het grondvlak en de hoogte van de cilinder zodat de inhoud van de cilinder maximaal is.

Heel erg hard bedankt voor uw hulp!

Yente
17-9-2016

Antwoord

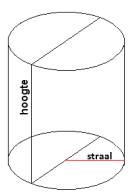
Je hebt de volgende formules nodig:

$\eqalign{
& {O_{cilinder}} = 2\pi {r^2} + 2\pi rh \cr
& {I_{cilinder}} = \pi {r^2}h \cr} $

Je weet dat de oppervlakte gelijk is aan 1 m². Dat geeft:

$2\pi {r^2} + 2\pi rh = 1$

Je kunt daarmee $h$ uitdrukken in $r$. Als je dan in de formule voor de inhoud de $h$ vervangt door je uitdrukking in $r$ dan heb je de inhoud uitgedrukt in $r$. Met de afgeleide kan je dan de waarde van $r$ bepalen voor de grootste oppervlakte.

Zou dat lukken?

WvR
17-9-2016