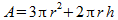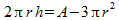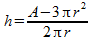|
|
|
\require{AMSmath}



Re: Extremaproblemen
Om h te isoleren komt men toch informatie te kort?
Ik heb A volledig = 4 pi r2 + 2 pi r (r+h)
maar die vergelijking is toch niet gelijk aan 0?
De totale inhoud = pi r2 h + 2/3 pi r3 waar men dan de h die men had geÔsoleerd moet invullen zodat enkel r de variabele is.. Ik weet echt niet hoe h af te zonderen...
joland
Student universiteit BelgiŽ - zondag 25 oktober 2015
Antwoord
Hallo Jolanda,
Volgens mij heb je een rekenfout gemaakt bij het opstellen van je formule voor de oppervlakte A. De totale oppervlakte bestaat uit:
Grondvlak (cirkel): pi∑r2
Cilindermantel: 2∑pi∑rh
Halve bol: 2∑pi∑r2
In totaal wordt dit:
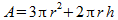
Isoleren van h gaat als volgt:
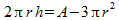
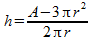
Vul dit in je vergelijking voor I in. De variabele h ben je nu kwijt. Je kunt verder met stap 5 uit mijn vorige antwoord.
Lukt het nu?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 oktober 2015
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 76616
Dit is een reactie op vraag 76616