WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Scores van de SAT-test

De scores van de SAT-Test heeft een normale distributie met een gemiddelde van 500 en een standaardafwijking van 100.

A)
als de middelbare school alleen studenten accepteert die score in de top 60% van deze test, wat is de minimum score die je nodig hebt om toegelaten te worden.

B)
wat is de minimum score die je nodig hebt om in de top 10% van deze distributie te zijn.

C)
welke scores vormen de grenzen voor het midden 50% van de distributie?

De antwoorden:

A. z = -0,25 en X=475
B. z = 1.28 en X=628
C. z = ±0.67 X=433 en X=567

Ik snap niet hoe ze op de z-scores komen. Ik snap wel hoe je de x-score uitrekent. In de bijlage vindt u een plaatje met alle z-scores en proporties. In het boek staat uitgelegd dat je bij dit soort vragen een normaal verdeling moet maken en dan moet aangeven welke deel van de normaalverdeling je wilt berekenen/zoeken. Je kan de z-score in de tabel opzoeken...
yalda
Student universiteit - zaterdag 26 september 2015

Antwoord

Uit de tabel:

A.

$
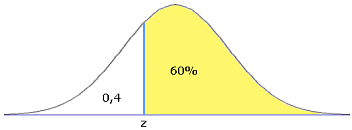
\eqalign{\frac{{X - 500}}
{{100}} = - 0,25 \Rightarrow X = 475}
$

B.

$
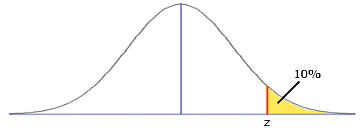
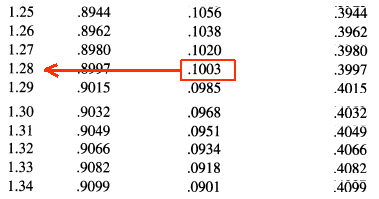
\eqalign{\frac{{X - 500}}
{{100}} = 1.28 \Rightarrow X = 628}
$

C.

$
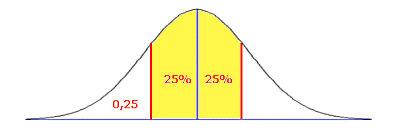
\eqalign{
& \frac{{X - 500}}
{{100}} = - 0,67 \Rightarrow X = 433 \cr
& \frac{{X - 500}}
{{100}} = 0,67 \Rightarrow X = 567 \cr}
$

Helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 26 september 2015