|
|
|
\require{AMSmath}
Re: Wiskunde Olympiade opgave 1994-A3
Bedankt voor de snelle reactie,
Klopt de congruentie dan op deze manier?
DP=PE (Want DP is in feite PE door de vouw)
PR=PR (gemeenschappelijk)
$\angle$RPE=$\angle$DPR (de hoek wordt gespiegeld in PQ door het vouwen)
$\Delta$PRE@DPR
Oscar
Leerling bovenbouw havo-vwo - vrijdag 3 juli 2015
Antwoord
Hallo Oscar,
Je redenatie klopt. Echter, wanneer je wilt noteren dat twee driehoeken congruent zijn, behoor je de hoekpunten zodanig te benoemen dat overeenkomstige hoekpunten op dezelfde plaats staan. De conclusie zou dus moeten zijn:
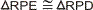
Nu is voor beide driehoeken de volgorde: rechte hoek - grote hoek - kleine hoek. De volgorde mag je zelf kiezen, maar voor beide driehoeken kies je wel dezelfde volgorde.
Wellicht dat de echte puristen om dezelfde reden de laatste overweging liever zo schrijven:
$\angle$RPE=$\angle$RPD
Dit heeft echter geen invloed op de grootte van de hoek, en dat is waar het hier om gaat.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 3 juli 2015
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 75974