WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Intersectie van 2 cilinders

Ik wil 2 buizen van verschillende diameters haaks op elkaar lassen. Hoe kan je de kromme berekenen om de intersectie te maken van de 2 buizen?
Eddy E
Iets anders - zondag 10 mei 2015

Antwoord

Hallo Eddy,

Kies de oorsprong van je assenstelsel in het snijpunt van de hartlijnen van je cilinders, en de assen langs deze hartlijnen, zie de figuur linksboven:

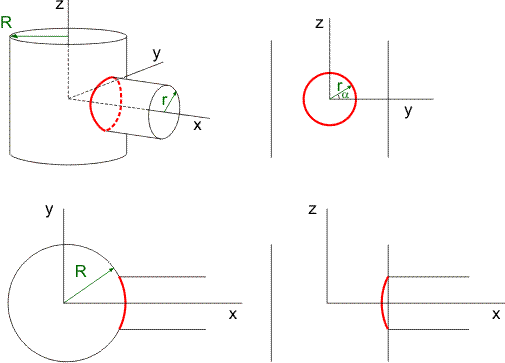
De straal van de buis met de grootste diameter noem ik R, de straal van de andere buis noem ik r.
In de figuur rechtsboven zie je de projecie in het y-z-vlak. De projectie van je intersectie is een cirkel met straal r. Er geldt dan:

y²+z²=r²

In de figuur linksonder zie je de projectie in het x-y-vlak. In dit vlak is de projectie van de intersectie een deel van een cirkel met straal R. Dus geldt ook:

x²+y²=R²

De intersectie wordt gevormd door de punten die voldoen aan deze twee vergelijkingen.
Wanneer je de eerste vergelijking van de tweede aftrekt, krijg je:

x²-z²=R²-r²

De projectie van de intersectie in het x-z-vlak is kennelijk een hyperbool, zie de figuur rechtsonder.

Je kunt de x-, y- en z-coördinaten van je intersectie ook weergeven in de vorm van een parametervoorstelling. Kies als parameter de hoek $\alpha$, zoals weergegeven in de figuur rechtsboven. In deze figuur zie je dan direct:

y = r·cos($\alpha$)
z = r·sin($\alpha$)

We vonden al:

x²+y²=R²

dus:

x² = R²-y²
x² = R²-r²cos²($\alpha$)
x = √(R²-r²cos²($\alpha$))

(De negatieve wortel is hier niet relevant, dit zou de doorsnijding weergeven wanneer de kleine buis links door de grote buis zou steken).

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 12 mei 2015