WisFaq!

Intersectie van 2 cilinders

Ik wil 2 buizen van verschillende diameters haaks op elkaar lassen. Hoe kan je de kromme berekenen om de intersectie te maken van de 2 buizen?

Eddy Everaerts
10-5-2015

Antwoord

Hallo Eddy,

Kies de oorsprong van je assenstelsel in het snijpunt van de hartlijnen van je cilinders, en de assen langs deze hartlijnen, zie de figuur linksboven:



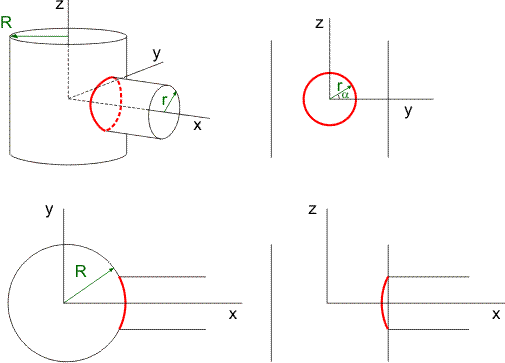
De straal van de buis met de grootste diameter noem ik R, de straal van de andere buis noem ik r.
In de figuur rechtsboven zie je de projecie in het y-z-vlak. De projectie van je intersectie is een cirkel met straal r. Er geldt dan:

y²+z²=r²

In de figuur linksonder zie je de projectie in het x-y-vlak. In dit vlak is de projectie van de intersectie een deel van een cirkel met straal R. Dus geldt ook:

x²+y²=R²

De intersectie wordt gevormd door de punten die voldoen aan deze twee vergelijkingen.
Wanneer je de eerste vergelijking van de tweede aftrekt, krijg je:

x²-z²=R²-r²

De projectie van de intersectie in het x-z-vlak is kennelijk een hyperbool, zie de figuur rechtsonder.

Je kunt de x-, y- en z-coördinaten van je intersectie ook weergeven in de vorm van een parametervoorstelling. Kies als parameter de hoek $\alpha$, zoals weergegeven in de figuur rechtsboven. In deze figuur zie je dan direct:

y = r·cos($\alpha$)
z = r·sin($\alpha$)

We vonden al:

x²+y²=R²

dus:

x² = R²-y²
x² = R²-r²cos²($\alpha$)
x = √(R²-r²cos²($\alpha$))

(De negatieve wortel is hier niet relevant, dit zou de doorsnijding weergeven wanneer de kleine buis links door de grote buis zou steken).

GHvD
12-5-2015