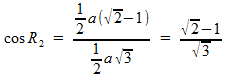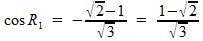|
|
|
\require{AMSmath}



Afstand van punt tot rechte
Gegeven: halfregelmatig antiprisma
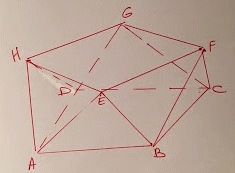
Gevraagd: d(G,AB)
Heeft u een idee?
Alvast bedankt!
Jasmin
3de graad ASO - maandag 4 mei 2015
Antwoord
Hallo Jasmine,
De lengte van de zijden van het grondvlak en bovenvlak noem ik a. Kies punt Q op het midden van AB, en R op het midden van CD. Teken dan het vlak door EGRS. Dit ziet er zo uit:
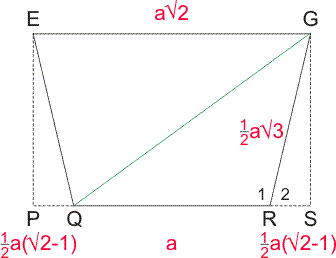
De gevraagde afstand is de lengte van de groene lijn GQ.
QR = a (dit is een zijde van het grondvlak).
EG = aÖ2 (dit is een diagonaal van het grondvlak)
Het verschil tussen deze lengtes wordt verdeeld over PQ en RS. Zo kunnen we berekenen:
RS = 1/2a(Ö2 - 1)
De zijvlakken van het antiprisma zijn gelijkzijdige driehoeken met zijde a. Het lijnstuk RG is de hoogte van zo'n driehoek. Je vindt:
RG = 1/2aÖ3
In de figuur zie je:
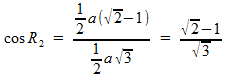
Dan is:
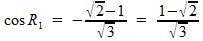
In driehoek QRG ken je nu de zijden QR en RG en de cosinus van de ingesloten hoek. Met de cosinusregel kan je de gevraagde zijde GQ berekenen.
Kan je hiermee verder?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 5 mei 2015
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|