WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Minimum berekenen

Dit is een reactie op vraag 75056

Ik probeer (x+y)² + 4xy $\leq$ 2 te veranderen in: x² + y² $\leq$ 2 - 8xy
Daarna vervang ik deze in A $\leq$ 3(x⁴ + y⁴ + x²y²) -2 ( 2-8xy)+ 1..
Ik weet het niet meer.

Ik snap het niet wat je mij uitlegt. Als je het verder uitwerkt dan begrijp ik beter. Alvast bedankt.

Son Tr
Student universiteit - dinsdag 24 maart 2015

Antwoord

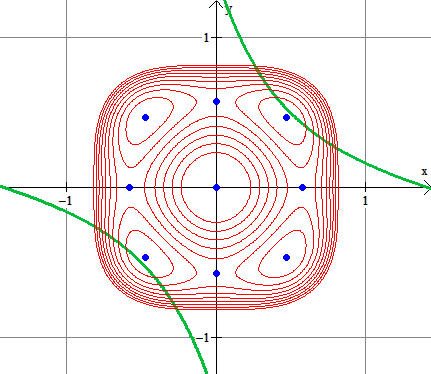
Zie het plaatje.
Je moet werken in het gebied tussen (en inclusief) de groene krommen.
Voor het gebied strikt tussen de krommen kunnen extremen alleen in de kritieke punten optreden; als het goed is kun je die zelf uitrekenen (het zijn de blauwe stippen in het plaatje). Daarnaast kunnen er extremen op de rand (de groene krommen dus) optreden; de kandidaatpunten kun je met de Laplace-methode opsporen of door $y$ in $x$ uit te drukken en dat in $A$ in te vullen.
NB
$$
y=-3x\pm\sqrt{8x^2+2}
$$

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 25 maart 2015