WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Kransen van regelmatige veelhoeken

Hoe kan ik de volgende formule bewijzen met formules van een regelmatige veelhoek?

$\alpha$ + (n-2)ß=(n-3)180°
Thibau
3de graad ASO - dinsdag 24 februari 2015

Antwoord

Hallo,

In de figuur hieronder is een krans van vijfhoeken getekend, gelijksoortige kransen van andere veelhoeken zijn ook mogelijk.

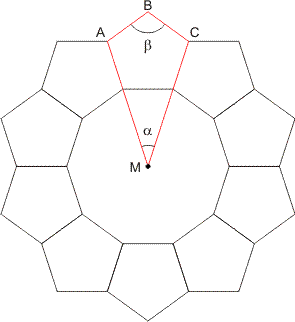
Het aantal hoeken van zo'n veelhoek noem ik n (in dit voorbeeld dus: n=5). Van één veelhoek verleng ik de twee zijden die de spiegelassen vormen naar het midden M van de krans. Zo ontstaat een nieuwe rode veelhoek MABC, het aantal hoeken hiervan is (n-1). Eén van deze hoeken is $\alpha$, de overige hoeken (dit zijn er dus n-2) zijn $\beta$. De som van de hoeken in de rode veelhoek is dus:

Som hoeken in rode veelhoek = $\alpha$ + (n-2)$\beta$

In het algemeen geldt dat de som van de hoeken in een veelhoek met k hoeken gelijk is aan (k-2)×180°. Het aantal hoeken van de rode veelhoek is één minder dan van de veelhoeken in de krans, dus:

k = n-1

De som van de hoeken in de rode veelhoek is dus (n-3)×180°.

Zodoende geldt dus:

$\alpha$ + (n-2)$\beta$ = (n-3)×180°

OK zo?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 25 februari 2015

Re: Kransen van regelmatige veelhoeken