In de figuur hieronder is een krans van vijfhoeken getekend, gelijksoortige kransen van andere veelhoeken zijn ook mogelijk.
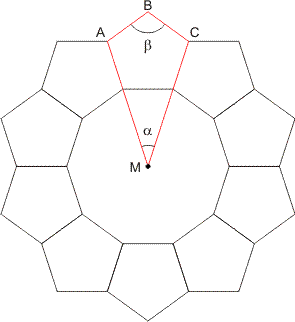
Het aantal hoeken van zo'n veelhoek noem ik n (in dit voorbeeld dus: n=5). Van één veelhoek verleng ik de twee zijden die de spiegelassen vormen naar het midden M van de krans. Zo ontstaat een nieuwe rode veelhoek MABC, het aantal hoeken hiervan is (n-1). Eén van deze hoeken is $\alpha$, de overige hoeken (dit zijn er dus n-2) zijn $\beta$. De som van de hoeken in de rode veelhoek is dus:
Som hoeken in rode veelhoek = $\alpha$ + (n-2)$\beta$
In het algemeen geldt dat de som van de hoeken in een veelhoek met k hoeken gelijk is aan (k-2)×180°. Het aantal hoeken van de rode veelhoek is één minder dan van de veelhoeken in de krans, dus:
k = n-1
De som van de hoeken in de rode veelhoek is dus (n-3)×180°.
Zodoende geldt dus:
$\alpha$ + (n-2)$\beta$ = (n-3)×180°
OK zo?
GHvD
25-2-2015