WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vergelijking raaklijn aan cirkel

Goedenavond,

Ik ben momenteel bezig met dit onderwerp maar kan er totaal niet uitkomen, zelfs niet met de uitleg in het boek.

De vraag : Bepaal een vergelijking van de raaklijn aan de gegeven cirkel in het gegeven punt A.

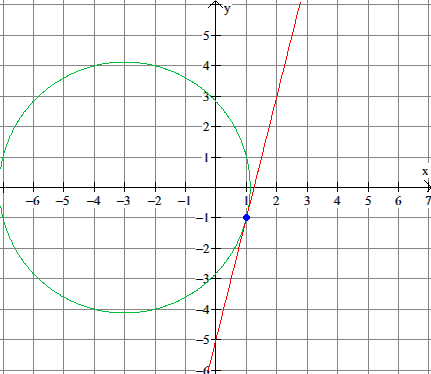
x²+y²+6x-8=0 , A = (1,-1)

Dit is mijn uitwerking:
(x+3)²+y²=17
M (middelpunt) = (-3,0)

M-A : -3 - 1 = -4 =x , 0 + 1 = y
Dus : -4x+y = ?
Als ik punt A hier invul dan krijg ik -4x-y=-5

Wat doe ik verkeerd? Bij voorbaat dank.
Michae
Student hbo - vrijdag 13 februari 2015

Antwoord

Op de een na laatste regel schrijf je $-4x-y=-5$ in plaats van $-4x+y=-5$. Doe je dat niet dat klopt het precies!

Een mooie methode staat op cirkel en raaklijn. Alles zullen we eerlijk delen.

De raaklijn door $A(1,-1)$ gaat door:

$x·1+y·-1+3x+3·1-8=0$
$x-y+3x-5=0$
$y=4x-5$

Al 's eerder gezien?
Zie Raaklijnen

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 13 februari 2015