WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Gelijkbenige driehoek bewijzen

Dit is een vraag waar ik al een tijdje mee bezig ben en ik kom er maar niet uit.

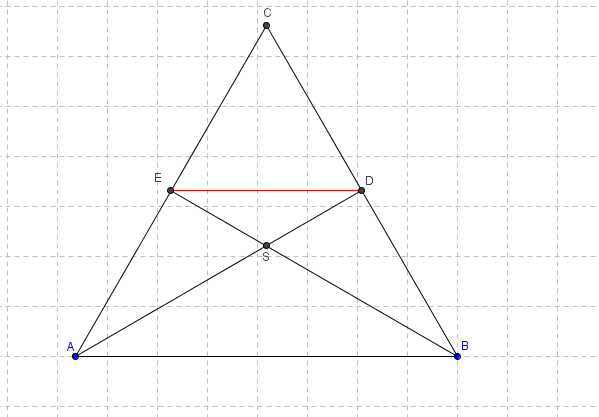
Gegeven is driehoek ABC met de zwaartelijnen AD en BE, waarbij |AD| = |BE|. Het snijpunt van deze zwaartelijnen is S. Bewijs dat driehoek ABC gelijkbenig is.
Kim
Leerling bovenbouw havo-vwo - dinsdag 3 februari 2015

Antwoord

Beste,
Het is nogal een opgave hoor, maar hier wat ik vond.

$
\begin{array}{l}
ED//AB{\rm{\,vanwege\,factor\,2\,uit\,C}} \\
\left. \begin{array}{l}
\angle BAD = \angle ADE \\
\angle EBA = \angle BED \\
Z - hoeken \\
\end{array} \right\}\Delta ASB \approx \Delta DSE \\
\frac{{ED}}{{AB}} = \frac{1}{2} = \frac{{DS}}{{AS}} = \frac{{ES}}{{BS}} \Rightarrow \left| {AS} \right| = \frac{2}{3}\left| {AD} \right| \wedge \left| {BS} \right| = \frac{2}{3}\left| {BE} \right| \\
\left. \begin{array}{l}
\left| {AS} \right| = \frac{2}{3}\left| {AD} \right| \\
\left| {BS} \right| = \frac{2}{3}\left| {BE} \right| \\
BE = AD \\
\end{array} \right\}AS = BS \Rightarrow \angle BAD = \angle ABE \\
\left. \begin{array}{l}
AD = BE \\
\angle BAD = \angle ABE \\
AB = AB \\
\end{array} \right\}\Delta BAD \approx \Delta ABE \Rightarrow AE = BD \\
\\
\end{array}
$

DvL

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 3 februari 2015

Re: Gelijkbenige driehoek bewijzen