WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Standaardafwijking pak suiker

Het gemiddelde van een pak suiker is 252,2 gram met een standaardafwijking van 1,2 gram
Het gewicht is normaal verdeeld.
a) Er is een voorraad van 560 pakken suiker. Hoeveel van deze hebben een gewicht tussen 251 en 252gram

b) 15% weegt meer dan dan X gram.
Wat is X? Bepaal deze
c) Met de gegeven (Griekse) u en o heeft 4% van de pakken suiker een gewicht onder de 250 gram. Dit vindt de winkelier onacceptabel en wil dat dit 1% is.
Wat moet o worden, zodat 1% van de pakken suiker eenggewicht heeft onder de 250 gram?

Hopelijk kan iemand mij helpen, want ik kom er niet achter...
Welke stappen moet ik op mijn GR nemen?
Sanne
Leerling bovenbouw havo-vwo - dinsdag 18 november 2014

Antwoord

Hallo Sanne,

Dit soort vragen kan je steeds terugbrengen tot hetzelfde standaard-type:
4 'dingen' spelen een rol:
de gemiddelde waarde m
de standaardafwijking s
twee grenzen (minimum en maximum waarde van de kansvariabele)
de kans p dat een willekeurige waarneming binnen deze grenzen valt
De structuur van de opgaven is dan:

3 van deze 4 zijn gegeven, bereken de 4^e

Vraag a)
m=252,2
s=1,2
linker grens: 251; rechter grens: 252
p=onbekend (dit is de vraag).
Deze berekening voer je uit met de functie NORMALCDF (of iets dat daarop lijkt, ik weet natuurlijk niet welke rekenmachine je precies hebt). Bij mijn wat oudere TI-84 vind ik deze functie onder 2ND®DISTR®optie 2 (het knopje VARS) en moet ik de getallen in de juiste volgorde intypen (linker grens, rechter grens, gemiddelde, standaardafwijking, dus: NORMALCDF(251,252,252.2,1.2)) Bij modernere rekenmachines kan je een menu invullen.

Ik vind: p(gewicht tussen deze grenzen)=0,2752. In een voorraad van 560 pakken is het aantal pakken met gewicht tussen deze grenzen:
560×0,2752 = 154

vraag b)
Nu weten we:
m=252,2
s=1,2
linker grens: onbekend, deze noemen we X; rechter grens: 10⁹⁹
p=0,15
(Eigenlijk moet de rechter grens oneindig zijn, we nemen het grootste getal dat de rekenmachine aankan: 10⁹⁹)

Helaas heeft onze rekenmachine geen standaaard functie om een onbekende grens te berekenen. Daarom laten we de rekenmachine een groot aantal waarden uitproberen, en bekijken we achteraf bij welke waarde van s 'toevallig' de juiste waarde van p wordt gevonden. Dit gaat als volgt:

Kies knopje 'y=', en voer in:
Y1=NORMALCDF(X,10^99,252.2,1.2)
Y2=0.15

Voordat je de grafiek laat tekenen, is het verstandig om redelijke waarden voor je window te kiezen. In dit geval zou je dit zo kunnen doen:

Maak altijd een schets van de normaalcurve, zet de gegevens hierin, arceer het gebied tussen linker en rechter grens.

Mijn schets ziet er zo uit:

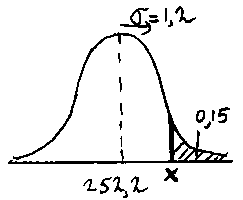
Bedenk wat de waarde van X ongeveer zou kunnen zijn. In dit geval is X de linker grens van het gearceerde gebied, de oppervlakte van dit gebied is 0,15. X is dus duidelijk groter dan de gemiddelde waarde 252,2. De horizontale afstand tussen gemiddelde en rechter kant van de figuur is hooguit 3 keer de standaarddeviatie, dus X ligt zeker tussen 252 en 256 (schat liever iets te ruim dan te krap). Voor het window kies ik dus:
XMIN=252
XMAX=256

De verticale richting is eenvoudiger: de uitkomst van NORMALCDF is een kans, deze ligt tussen 0 en 1. De belangrijkste waarde is de gegeven kans p=0,15. Wanneer ik kies:
YMIN=0
YMAX=0,30
dan komt deze belangrijke waarde precies in het midden van mijn scherm.

Plot nu de grafieken Y1 en Y2 (GRAPH). Je ziet hoe je rekenmachine de functie Y1=NORMALCDF tekent, met allerlei waarden van X tussen 252 en 256. Ook tekent je GR de horizontale lijn Y2=0,15. Het snijpunt van deze grafieken is bij de waarde van X die 'toevallig' goed is. Bereken dus het snijpunt (2ND®CALC®intersect), je vindt de waarde X=253,4.

vraag c)
Nu weten we:
m=252,2
s=onbekend, deze noemen we X
linker grens: -10^99; rechter grens: 250
p=0,01

Pak dit op dezelfde manier aan als vraag b. Nu is de onvekende X een standaardafwijking. De kleinst mogelijke waarde is natuurlijk 0, uit de vraag blijkt dat s kleiner moet worden dan 1,2. Kies voor het plotten dus XMIN=0 en XMAX=1,2. Vanwege de kleine p=0,01 mag YMAX ook wel wat kleiner dan bij vraag b, bijvoorbeeld YMAX=0,02.
Ik vind: s=0,95. Jij ook?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 18 november 2014

Re: Standaardafwijking pak suiker