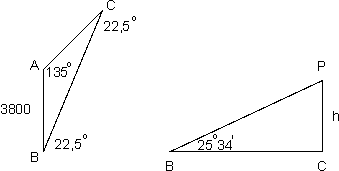WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Lengte van driehoeken berekenen

Uit een punt A ziet men een ballon in het N.O onder een hoek van 25°34` met het horizontale vlak; 3800 m zuidelijk van A ligt B. Van uit punt B ziet men de ballon in het N.N.O. Hoe hoog bevindt zich op dat moment de ballon?

Rebecc
Leerling bovenbouw havo-vwo - vrijdag 7 november 2014

Antwoord

Hallo Rebecca,

Laten we eerst de situatie van boven bekijken, zie de linker figuur:

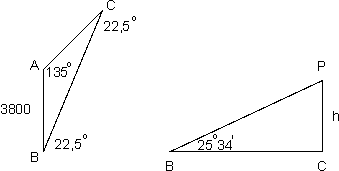
A en B zijn de gegeven punten, C is de plaats waar de ballon zich bevindt. B ligt 3800 meter ten zuiden van A. Vanuit A ligt C in het noord-oosten. Dat is precies tussen noord en oost in, dus op papier onder 45° omhoog. Hoek A wordt hiermee 135°.

Dan hoek B: vanuit B ligt C in het noord-noord-oosten, dat is weer precies tussen noord en noord-oost in. Dus vanuit B schuin omhoog met een hoek die de helft is van 45°. Hoek B is dus 22,5°. Omdat de hoeken A, B en C samen 180° zijn, vinden we voor hoek C ook 22,5°.

Met behulp van de sinusregel kan je de afstand BC uitrekenen.

Hierna bekijken we het verticale vlak, zie de rechter figuur. BC loopt horizontaal, de ballon hangt recht boven C in punt P. Je zoekt nu de afstand PC (is hoogte h van de ballon). Hoek B is 25°34'. Nu gebruiken we:

tan(B) = PC/BC

BC heb je net uitgerekend, de tangens van B kan je met je rekenmachine bepalen, dus PC kan je uitrekenen.

Lukt het hiermee?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 8 november 2014