|
|
|
\require{AMSmath}



Afgelegde weg berekenen mbv cosinusfuctie
Een voorwerp beweegt op een horizontale as. Zijn positie x (uitgedrukt in meter) wordt als functie van de tijd t (in seconden) gegeven door x(t) = cos($\pi$t/20).
Bereken de lengte van de weg die het voorwerp aflegt gedurende de eerste 15 seconden. (Het juiste antwoord is 1,5m)
Alvast bedankt.
Alexan
Student universiteit België - zaterdag 18 oktober 2014
Antwoord
Beste Alexander,
Het voorwerp maakt een harmonische beweging rond x=0. De amplitude is 1 meter, de periodetijd is 40 seconden. Onderstaande grafiek geeft de positie weer van het voorwerp op de x-as:
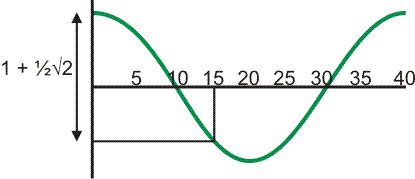
De gevraagde afgelegde weg wordt weergegeven door de verticale pijl links in de figuur.
Deze afgelegde weg s in de eerste 15 seconden vind je door te berekenen:
s = x(15) - x(0)
s = cos(15/20$\pi$) - cos(0)
s = -1/2√2 - 1
Het min-teken betekent dat het voorwerp in negatieve x-richting is verplaatst. De afgelegde weg rekenen we vaak positief, ongeacht de richting.
Het voorwerp beweegt dus van x=1 naar x=-1/2√2, totaal dus afgelegd:
Afgelegde weg = 1 + 1/2√2 meter.
Het door jou gegeven antwoord (s = 1,5 meter) is volgens mij onjuist.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 18 oktober 2014
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|










