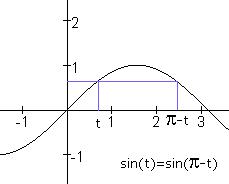WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Voorbeelden I

Dit is een reactie op vraag 72947

Maar voor de tweede oplossing moet je toch $2\pi-$de eerste oplossing doen? Dus $\frac{1}{6}\pi$? Dus ik dacht - - is + vandaar $2\frac{1}{6}\pi$
josine
Leerling bovenbouw havo-vwo - maandag 12 mei 2014

Antwoord

Nee, dat was bij de cosinus. Bij de sinus heb je $x$ en $x-\pi$. Dus zoiets als:

$sin(x)=\frac{1}{2}$
$x=\frac{1}{6}\pi$ of $x=\pi-\frac{1}{6}\pi$

of ook:

$sin(x)=-\frac{1}{2}$
$x=-\frac{1}{6}\pi$ of $x=\pi--\frac{1}{6}\pi$

Bedoel je dat?

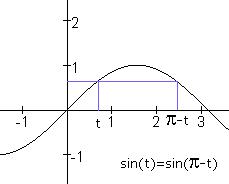
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 12 mei 2014

Re: Re: Voorbeelden I