WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Biljarten

De afmetingen van een biljarttafel zijn ,binnenkant genomen, in lengte 284,5 cm en de breedte 142,25 cm. Een bal wordt gestoten onder een hoek van 30° vanop een aangegeven plaats( neem links onder op de lengte 102 cm en op de breedte 53 cm (de coördinaten van het afstootpunt A zijn dus: A(102,53).

Op welke plaats botst de bal een tweede maal?
Welke afstand legt de bal af tussen de eerste en derde botsing met de banden?

Noem ik punt C de eerste botsing dan is cos30°=102/AC
AC= 102/cos30°= 117,78 cm
De bal botst in C onder 30°(gegeven) .Komt hij dan terug onder 30° en rolt zo naar punt D op de lange band. En dan verder naar het derde punt E.
Hoe moet het nu verder? Graag wat hulp indien er tijd voor bestaat.
Groeten
Rik Le
Iets anders - woensdag 2 oktober 2013

Antwoord

Hoi Rik,

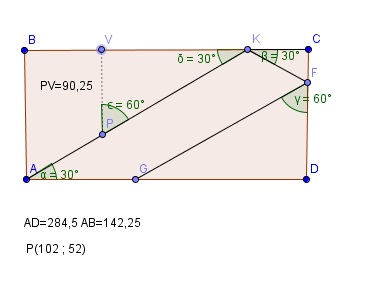
Ik heb besloten om het niet helemaal voor te rekenen, maar heb wel mooie schets voor je gemaakt. Bij biljarten is de hoek van inval gelijk aan de hoek van uitval. De baan die de bal maakt p-k-f-g

In driehoek pvk kun je vk uitrekenen met bijvoorbeeld de sinusregel.
KC=VC-VK (VC weet je vanwege coordinaat punt P

KF bereken je met cosinus(b) en lengte KC zo bereken je met de sinus ook CF en daaruit volgt DF.

Tot slot nog een keer de cosinus gebruiken om GF te berekenen. En de boel optellen.

Ik neem aan dat dat allemaal wel lukt, en ik vermoedde dat je slechts de schets helder wilde hebben?

mvg DVL

DvL

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 3 oktober 2013