|
|
|
\require{AMSmath}



Vergelijking sinuso´de opstellen
Ik heb een vraagstuk, bepaal de vergelijking van de sinuso´de door het punt (0,-31/2),die daarna eerst stijgt en met bereik[-6,-1] en waarvan de periode 4 is.
Mijn stappen zijn:
algemene vergelijking:
f(x)= asinb(x-c)+d
Evenwichtstand is y =6, het midden van -6 en -1
Amplitude is = 6 tot 1 = -5
De periode is 4= is ook 2p/b dus b= 2p/4 = 1/2p
Vanaf hier twijfel ik ofdat ik het wel goed doe:
c=0
y=-31/2 =d
a= -5, b= 1/2p, c =0 d= -31/2
y= -5 sin (1/2p(x-0))+ 31/2
Zou u mij kunnen en willen helpen, vanaf waar ik twijfel? Ik heb het idee dat het daar fout gaat. Heb ook op internet al info opgezocht, maar het wilt niet lukken vanaf dat 'stukje'.
Yvette
Iets anders - donderdag 27 juni 2013
Antwoord
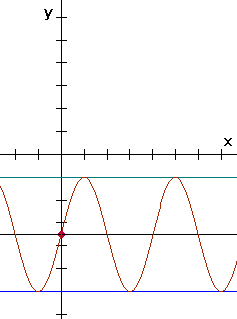
De evenwichtsstand is y=-31/2 (d). De amplitude is 21/2 (a). De periode is 1/2p (b). De horizontale verplaatsing is 0 (c). De formule wordt dan:
y=21/2Ěsin(1/2px)-31/2
Meer moet het niet zijn, maar je moet wel een beetje preciezer zijn...
Maar 't gaat steeds beter toch?
PS
De amplitude is dus de helft van het verschil tussen maximum en minimum. Het is de uitslag t.o.v de evenwichtslijn. Dus 2,5 naar boven, 2,5 naar beneden, dus de amplitude is 2,5.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 27 juni 2013
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|











