Ik heb een vraagstuk, bepaal de vergelijking van de sinusoïde door het punt (0,-31/2),die daarna eerst stijgt en met bereik[-6,-1] en waarvan de periode 4 is.
Mijn stappen zijn:
algemene vergelijking:
f(x)= asinb(x-c)+d
Evenwichtstand is y =6, het midden van -6 en -1
Amplitude is = 6 tot 1 = -5
De periode is 4= is ook 2p/b dus b= 2p/4 = 1/2p
Vanaf hier twijfel ik ofdat ik het wel goed doe:
c=0
y=-31/2 =d
a= -5, b= 1/2p, c =0 d= -31/2
y= -5 sin (1/2p(x-0))+ 31/2
Zou u mij kunnen en willen helpen, vanaf waar ik twijfel? Ik heb het idee dat het daar fout gaat. Heb ook op internet al info opgezocht, maar het wilt niet lukken vanaf dat 'stukje'.Yvette
27-6-2013
De evenwichtsstand is y=-31/2 (d). De amplitude is 21/2 (a). De periode is 1/2p (b). De horizontale verplaatsing is 0 (c). De formule wordt dan:
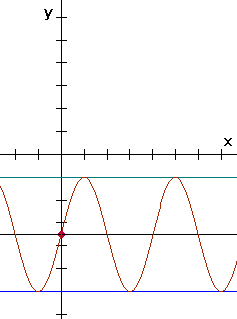
y=21/2·sin(1/2px)-31/2
Meer moet het niet zijn, maar je moet wel een beetje preciezer zijn...
Maar 't gaat steeds beter toch?
PS
De amplitude is dus de helft van het verschil tussen maximum en minimum. Het is de uitslag t.o.v de evenwichtslijn. Dus 2,5 naar boven, 2,5 naar beneden, dus de amplitude is 2,5.
WvR
27-6-2013
#70564 - Goniometrie - Iets anders
