|
|
|
\require{AMSmath}



De drie situaties bij het oplossen van vergelijkingen
Hoi,
In mijn boek staat dat als je een snijpunt wilt berekenen van twee lijnen dat je een vergelijking moet opstellen en dat je dan 3e situaties hebt maar ik snap niet wat ze bedoelen met de 3 situaties in het boek. dit zijn de 3e situatie:- er is één oplossing. De lijnen snijden elkaar
- er is geen oplossing. De lijnen zijn evenwijdig
- er zijn oneindig veel oplossingen, de lijnen vallen samen
Maar wanneer heb je welke want als ik alles doe en ik op het punt kom om een van deze 3 situaties te kiezen dan weet ik niet wanneer ik kan zeggen dat het 1 oplossing is, geen oplossing of oneindig veel. Zou u dit kunnen uitleggen?
Groetjes
alice
Leerling onderbouw vmbo-havo-vwo - donderdag 19 april 2012
Antwoord

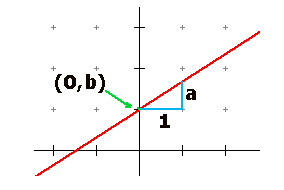 Bij de algemene formule voor een lineair verband tussen x en y hoort een formule van de vorm: Bij de algemene formule voor een lineair verband tussen x en y hoort een formule van de vorm:
y = ax + b
De grafiek van y=ax+b is een lijn die:- 1 naar rechts en a omhoog gaat
- de y-as snijdt in het punt (0,b)
- de waarde van a noemen we richtingcoëfficiënt.
Wanneer snijden twee lijnen elkaar niet? Als ze evenwijdig lopen, dus als de richtingcoëffiënten gelijk zijn. Ze kunnen dan ook nog samenvallen. Dan lopen ze evenwijdig en vallen dan precies samen. Als de rico's niet hetzelfde zijn dan snijden tewe lijnen elkaar altijd ergens.
Voorbeeld 1
y=2x+4 en y=3x+10 snijden elkaar want a=2 en a=3 en dat is niet gelijk.
Voorbeeld 2
y=2x+2 en y=2x-4 lopen evenwijdig a=2 en a=2 en dat is gelijk. Ze gaan niet door hetzelfde punt op de y-as want b=2 en b=-4
Voorbeeld 3
y=3x+1 en y=3x+1 vallen samen want a=3 en a=3 en b=1 en b=1.
Zoiets moet het zijn!

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 19 april 2012
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|









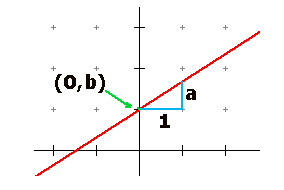 Bij de algemene formule voor een lineair verband tussen x en y hoort een formule van de vorm:
Bij de algemene formule voor een lineair verband tussen x en y hoort een formule van de vorm:
