|
|
|
\require{AMSmath}
Re: Re: Maximum bepalen met partiële afgeleiden
Ik krijg nu de volgende antwoorden:
{x = 1, alpha = 1/2·Pi},
{x = -1, alpha = 1/2·Pi},
{x = 1/3, alpha = -1/2·Pi}
Als ik deze waarden weer in de oorspronkelijke formule in vul, krijg ik 3 keer als uitkomst 0. Dat zou betekenen dat de maximale inhoud van de goot 0 is en dat klopt dus niet...
Martij
Student hbo - dinsdag 25 oktober 2011
Antwoord
het nul stellen van de bovenste partiele afgeleide (naar x) kan worden vereenvoudigd tot:
(4-8x) + (4x-4)·sin(y) = 0
Hieruit volgt:
sin(y) = (8x-4)/(4x-4)
In de onderste partiele afgeleide (naar y dus) kan (cos(y))2 geschreven worden als 1-(sin(y))2. Je bent nu van cos(y) af en kan voor sin(y) bovengenoemde breuk substitueren. Ik kom dan op deze formule:
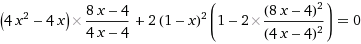
Dit levert x=1 of x=1/3
x=1 levert in de oorspronkelijke formule nul op voor elke waarde van y (en vervalt als oplossing, vermoed ik)
x=1/3 levert bij mij op: sin(y)=0,5 (dus y=$\pi$/6)
en als uitkomst van de oorspronkelijke formule: 0,385....
Kan dit kloppen?
GHvD
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 25 oktober 2011
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 65993