WisFaq!

Re: Re: Maximum bepalen met partiële afgeleiden

Ik krijg nu de volgende antwoorden:
{x = 1, alpha = ¹/₂·Pi},
{x = -1, alpha = ¹/₂·Pi},
{x = 1/3, alpha = -¹/₂·Pi}
Als ik deze waarden weer in de oorspronkelijke formule in vul, krijg ik 3 keer als uitkomst 0. Dat zou betekenen dat de maximale inhoud van de goot 0 is en dat klopt dus niet...

Martijn
25-10-2011

Antwoord

het nul stellen van de bovenste partiele afgeleide (naar x) kan worden vereenvoudigd tot:

(4-8x) + (4x-4)·sin(y) = 0

Hieruit volgt:

sin(y) = (8x-4)/(4x-4)

In de onderste partiele afgeleide (naar y dus) kan (cos(y))² geschreven worden als 1-(sin(y))². Je bent nu van cos(y) af en kan voor sin(y) bovengenoemde breuk substitueren. Ik kom dan op deze formule:



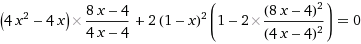
Dit levert x=1 of x=1/3

x=1 levert in de oorspronkelijke formule nul op voor elke waarde van y (en vervalt als oplossing, vermoed ik)
x=1/3 levert bij mij op: sin(y)=0,5 (dus y=$\pi$/6)

en als uitkomst van de oorspronkelijke formule: 0,385....

Kan dit kloppen?

GHvD
25-10-2011