WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Grote straat gooien Yahtzee

Dit is een reactie op vraag 65404

Dit hadden wij zelf ook bedacht, echter vergeet je mee te nemen dat bij situatie 2 je ook kans hebt om 1,2,3,4,5 te gooien. De 3 dobbelstenen moeten dus 2 en 4 worden, en óf 1 óf 6. Hierdoor wordt de kans toch groter? Bovendien heb je met 3 dobbelstenen meer kans om 2 of 4 te gooien dan met 2 dobbelstenen.

Alvast bedankt,

Francesco
France
Student universiteit - donderdag 21 juli 2011

Antwoord

Dag Francesco,

Inderdaad. Als je bij situatie 2 de 1 weer meeneemt om te dobbelen, kun je inderdaad evengoed ook op 1,2,3,4,5 uitkomen. Bij de situatie dat je 1 dus weer meeneemt, heb je twee gunstige gevallen: je komt uit op 1,2,3,4,5 of op 2,3,4,5,6.

Dan weer verder te beredeneren vanaf situatie 2: Je neemt de dobbelstenen 1, 3 en 5 weg (zodat je nog 3 en 5 hebt liggen). Die drie dobbelstenen die je in je hand hebt (of in het bekertje eigenlijk he), die moeten dus óf 1, 2 en 4 worden, óf ze moeten 2, 4 en 6 worden. (of of, in de kansrekening doe je dan plus): P([1,2 en 4] of [2,4 en 6]) = P(1,2,4)+P(2,4,6)=1/36 + 1/36 = 1/18

Je begon dus met 1,3,3,5,5.
Neem je de 3 en 5 weg, dan had je een kans van 1/18 om en grote straat te gooien (1,2,3,4,5)
Neem je de 1, 3 en 5 weg, dan heb je klaarblijkelijk ook een kans van 1/18 om een grote straat te gooien (1,2,3,4,5 óf 2,3,4,5,6).

Het maakt dus niks uit of je 1 wel of niet meeneemt. De kans op een grote straat met drie dobbelstenen (als je al 3 en 5 hebt liggen) is even groot als de kans op een grote straat met twee dobbelstenen (als je al 1, 3 en 5 hebt liggen).

Je kunt ook alle mogelijkheden uittekenen om zekerheid te hebben van deze berekeneningen (bijvoorbeeld via een kansboom).

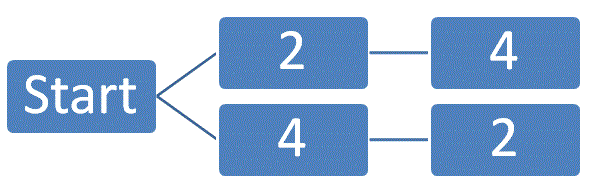
Situatie 1 Met twee dobbelstenen gooien tot een grote straat (1, 3 en 5 liggen al). Iedere weg levert een kans van 1/36. Alle wegen (mogelijkheden) samen leveren dus een kans van 2/36 = 1/18

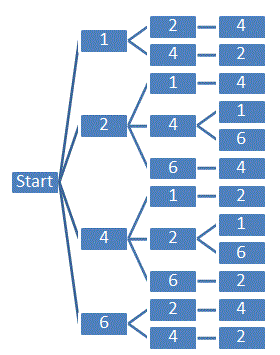
Situatie 2 Met drie dobbelstenen gooien tot een grote straat (3 en 5 liggen al). Iedere weg levert een kans van 1/216. Alle wegen (mogelijkheden) samen leveren dus een kans van 12/216 = 2/36 = 1/18

Dankjewel voor de opmerking.

Hopelijk is dit antwoord naar voldoening? Het maakt dus niks uit of je 1 wel of niet meeneemt (als je 1,3,3,5,5 hebt liggen)

Met vriendelijke groet,

Thijs Bouten

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 22 juli 2011