WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Teken in het (x,y)-vlak de volgende formules

Dit is een reactie op vraag 65365

Beste Lieke,

Het is voor mij nog niet helemaal duidelijk, ik heb nu namelijk de verticale asymtoten op 1 en -1 gezet. Vervolgens gebruik ik voor e 2.71... op de x as als horizontale asymtoten. Nu heb ik 4 asymtoten die zorgen voor een vierkant, geen driehoek. Ik snap niet hoe ik hierin de juiste lijnen teken.

Vervolgens dien ik een vergelijking van deze 2 grafieken te maken om de snijpunten te berekenen. dus ln x = -ln x, wat zijn hiervoor de reken regels.

Bij voorbaat dank.
Groetjes,
Marloes.
p.s ik mag geen gebruik maken van mijn grafische rekenmachine.

Marloe
Leerling bovenbouw havo-vwo - donderdag 7 juli 2011

Antwoord

Beste Marloes,
Teken eerst de grafieken van y=ln(x) en y=-ln(x), die hebben een verical asymptoot bij x=0 en niet bij x=1 of -1.Hun snijpunt moet je inderdaad bepalen, maar dat is bij x=1 en y=0. Er zijn geen horizontale asymptoten.
Verder teken je de verticale lijn x=e. Dan ontstaat er echt een soor triehoek!
Zie plaatje.
De rekenregels die je nodig hebt voor het snijpunt zijn gewoon: ln(x)=-ln(x) geeft 2ln(x)=0, of ln(x)=0 en dan moet gelden: x=e⁰, en dat is 1.
Maar als je ziet dat de grafieken elkaars spiegelbeeld zijn in de x-as kan er alleen maar een snijpunt zijn, bij y=0.

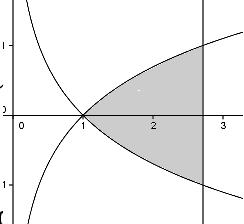
Helpt dat?
Succes, Lieke.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 10 juli 2011