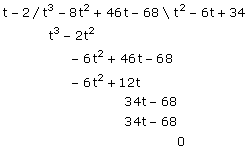|
|
|
\require{AMSmath}



Nulpunten polynoom
gegeven nulpunten: t=0 en t=2
polynoom:
t4-8t3+46t2-68t
berekenen dmv een staartdeling.
bij t=2
(t-2)/(t4-8t3+46t2-68t)\ Ik kom tot t3+5t2+56t en hou 44 over, hoe moet dit verder?
bij t=0
t/(t4-8t3+46t2-68t)\ t3-8t2+46t-68
Hoe dien ik dit uit te werken?
En hoe kom ik tot die nulpunten, als die er al zijn?
mug55
Student universiteit - woensdag 22 juni 2011
Antwoord
t4-8t3+46t2-68t kan je schrijven als:
t(t3-8t2+46t-68) omdat t=0 een nulpunt is.
t3-8t2+46t-68 kan je gaan schrijven als
(t-2)(....) omdat t=2 een nulpunt is.
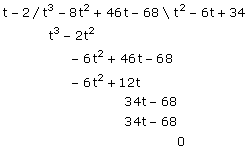
De vraag is nu of je t2-6t+34 nog verder zou kunnen ontbinden. Maar daar heb je dan waarschijnlijk wel 's de som-product voor geleerd? Dat gaat niet lukken!
Conclusie: t4-8t3+46t2-68t=t(t-2)(t2-6t+34)
Hopelijk helpt dat!

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 22 juni 2011
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|