WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Gelijkvormige driehoeken

GEGEVEN XYZ met |XY| = |XZ|
m = ml |XY|
doorsnede m en lijnstuk |YZ| = P

BEWIJS DAT |XY|² = |YZ| maal |PX|

hartelijk bedankt
Thibau
2de graad ASO - donderdag 9 januari 2003

Antwoord

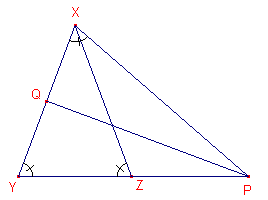
We gebruiken dus gelijkvormigheid van driehoeken.
Het "te bewijzen" maakt het in ieder geval noodzakelijk het lijnstuk PX in de beschouwingen te betrekken.
En dan wordt het in de eerst plaats zoeken naar gelijke hoeken.
Kijk nu eens naar driehoek PXY.
PQ is daarin middelloodlijn.
Waarom is nu PXY ook een gelijkbenige driehoek?
Dan is de conclusie snel getrokken dat hoek(Y) = hoek(YXP).
Bekijk nu de driehoeken XYZ en PXY.
Waarom zijn deze gelijkvormig?
Dan geldt: XY : PX = YZ : XY.
En dan staat er wat je wilde bewijzen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 9 januari 2003