|
|
|
\require{AMSmath}



Raaklijnen aan cirkel
Hallo Wisfaq,
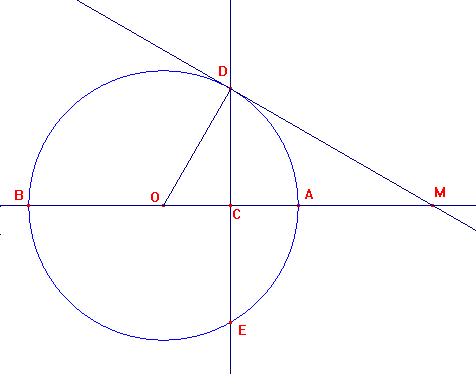
|AB| is een middellijn van C(O,r)
De middellijn van |AO| snijdt de cirkel in D en E
M is het puntspiegelbeeld van O om A
Bewijs nu dat MD en ME raaklijnen zijn aan de cirkel.
Een figuur en wat uitleg graag aub....
Groeten,
Rik
Rik Le
Iets anders - zondag 16 januari 2011
Antwoord
Uit de constructie volgt dat :
|OC| = r/2 ; |CM| = 3r/2 ; |OD| = r en |OM| = 2r
In de driehoek OCD volgt : |CD|2 = |OD|2 - |OC|2 =
r2 - r2/4 = 3r2/4
(Pythagoras)
In de driehoek CMD volgt : |DM|2 = |CD|2 +|CM|2 = 3r2/4 + 9r2/4 = 3r2
Daaruit volgt : |OM|2 = |OD|2 + |DM|2, want 4r2 = r2 + 3r2
en dus is driehoek ODM rechthoekig in D
De rechte DM staat dus loodrecht op de straal OD en is dus raaklijn.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 16 januari 2011
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










