WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Omgeschreven cirkel van een driehoek

Goede avond,
Gegeven:
1) driehoek ABC
2) Cirkel C(0,r) is omgeschreven aan de gegeven driehoek.
3) m=ML[A](middelloodlijn van 0A= straal cirkel C(0,r))
Bewijs nu:
S(m)(C(0,r) is de omgeschreven cirkel van S(m)(driehoek ABC)
Een constructie kan ik niet geven....
Graag wat uitleg aub.
Groeten,
Rik
Rik Le
Iets anders - dinsdag 11 januari 2011

Antwoord

Dag Rik,

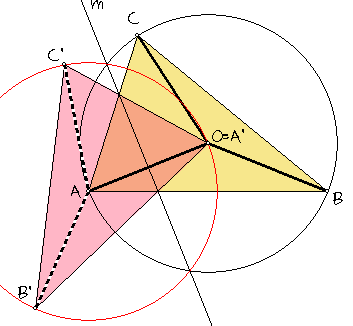
Als met S(m) de spiegeling in de lijn m (de middelloodlijn van OA) wordt bedoeld, dan is:
S(m)(A) = A' = 0, S(m)(B) = B', S(m)(C) = C'
en ook:
S(m)(O) = A
Dan is OA = r = AA', OB = r = AB' en OC = r = AC'.
Aangezien een cirkel bepaald is door drie punten, is de cirkel met middelpunt A en straal r de omgeschreven cirkel van driehoek A'B'C'.
En deze cirkel is tevens het S-beeld van de omgeschreven cirkel van driehoek ABC.

Groet, DK

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 12 januari 2011