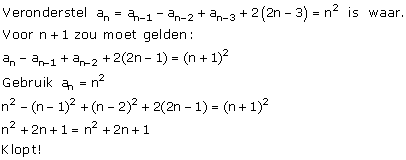WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Inductie

Dit is een reactie op vraag 63353

Ah oke! ja nou wat ik dus had gedaan was dit:
a₁=1²=1
a₂=2²=4
a³=3²=9
Hieruit heb ik dus al een vermoeden dat het an=n² is voor elk positief geheel getal met n groter/gelijk aan 4. Vervolgens ga ik dus 4 invullen in die hele lange formule van an. daar krijg ik 16 uit. Datzelfde heb ik gedaan voor n is 5 en n is 6. (Maar blijkbaar moest het alleen voor 4 ??) 4 is het kleinst mogelijk getal bij deze formule en daarbij zie ik dat mijn vermoeden hierbij iig wel geldt. Vervolgens wist ik dus niet wat ik er verder mee moest want ik moet natuurlijk nog wel bewijzen dat het zo is. Maar wat ik dus uiteindelijk heb gedaan is: Ik ben verder gegaan met inductie. Aangezien a₁=1²=1 voor n=1. en ai:i² voor elke geheel positieve getal met i groter gelijk aan 1 en i kleiner gelijk aan k. Dan laten we zien dat a(k+1) = (k+1)². en die k+1 vul ik dus helemaal in die lange formule in en dan krijg ik er (k+1)² uit. en vervolgens heb ik dus bewezen dat an=n² voor alle n van alle gehele getallen. Dat denk ik ?

Heel erg bedankt voor het helpen!:D
S
Student universiteit - maandag 25 oktober 2010

Antwoord

Je hebt vastgesteld dat a₄=16. Als je nu kan aantonen dat je vermoeden voor n+1 waar is als het waar is voor n dan ben je er. Het domino-effect, zullen we maar zeggen.

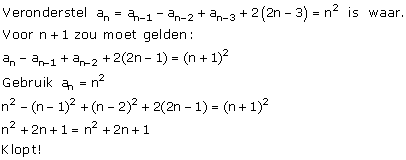
Dus dan ben je er wel, denk ik...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 25 oktober 2010