WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Periodieke functies

De diepte van de vaargeul is voor de scheepvaart van groot belang. Door de werking van eb en vloed varieert deze diepte met de tijd. voor Antwerpen kan de diepte van de vaargeul benaderend worden beschreven met behulp van het verband: d(t)= 2,5sin t/2 +8. Hierbij is d uitgedrukt in meter en t in uur

1. plot de grafiek in d

2. hoelang mag een schip met een diepgang van 7 meter erover doen om de haven binnen te varen? Een schip heeft onder de kiel nog 20% van zijn diepgang aan water nodig om veilig te kunnen varen

3. bereken daarna de diepgang welke een schip maximaal mag hebben om veilig de haven te kunnen binnenvaren als je weet dat de reis van de ingang van de haven tot de aanlegsteiger anderhalf uur duurt.
Eva
3de graad ASO - zaterdag 16 oktober 2010

Antwoord

1.

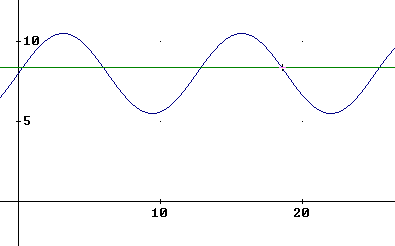
2.
De minimale waterhoogte is 8.4 meter.
Aflezen of bereken van de snijpunten van d en y=8.4 geeft:
t = 0.3213813059 en t = 5.961804001
De maximale tijd is ongeveer 5.6 uur.

3.
De maximale waterhoogte is 2,5sin((pi-0.75)/2)+8. Dat is dan ongeveer 10,3 meter. Rekeninghoudend met de 20% extra ruimte onder de kiel geeft dit ongeveer 8,6 meter als maximaal mogelijke diepgang.

Hopelijk helpt dat...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 16 oktober 2010

Re: Periodieke functies