|
|
|
\require{AMSmath}
Overschrijdingskansen
Ik loop al een tijdje te hannessen met het rekenen aan de normale verdeling, maar bij overschrijdingskansen loop ik helemaal vast.
De opgave luidt als volgt:
Gegeven P(|Z-0.5| c)=0.05
Bereken c
de afgelopen 11/2 uur waren vruchteloos, dus hopelijk kan iemand me helpen.
Alvast bedankt.
Karel
Leerling bovenbouw havo-vwo - maandag 4 oktober 2010
Antwoord
Neem 's aan dat je c zou kennen, zou je dan de kans op P(|Z-.5|c) uit kunnen rekenen?
Neem c=1. Gevraagd P(|Z-.5|1).
|Z-.5|1 Þ Z-.5 -1 of Z-.51. Z-.5 of Z1.5.
P(|Z-.5|1)=P(Z-.5)+P(Z1.5) 0.309+0.067=0.376
Neem c. Gevraagd P(|Z-.5|c).
|Z-.5|c Þ Z-.5-c of Z-.5c. Z-c+.5 of Zc+.5.
P(|Z-.5|c)=P(Z-c+.5)+P(Zc+.5)=0.05
P(-c+.5Zc+.5)=0.95
Nu maar 's een tekening maken!
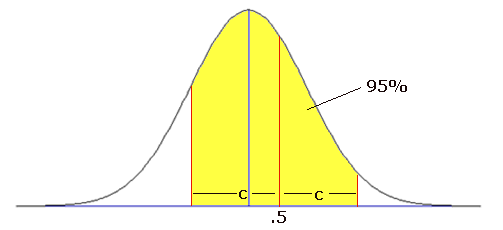
De vraag is nu hoe bereken je P(-c+.5Zc+.5)?
Met je GR kan je een tabel maken!
Met Y1=normalcdf(-X+.5,X+.5,0,1)
 
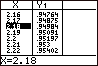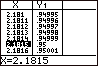
Zodat c=2.1815
Zoiets? Ik kan me alleen niet voorstellen dat dit nu de bedoeling was van het vraagstuk!? Heb je er ook antwoorden bij? Klopt het?
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 5 oktober 2010
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
