|
|
|
\require{AMSmath}



Vergelijking
Hallo,
ik heb gisteren een tentamen gehad wil laten controleren of ik het goed heb gedaan.
vraag 1
a) Ö(x2-5)= 2. Ik heb als antwoord x= 3 of -3
b) 35/(x-3)2= 5. Ik heb als antwoord 5,6457. (Ö van 7 en dan + 3)
vraag 2
a) schets in 1 figuur de grafieken van de functies.
f(x)= x + 2/4 g(x)= 4/x+2
b) bereken alle snijpunten van de grafieken van f en g
ik had hier (-6,-1) en (2,1)
c)voor welke waarden van x is f(x) kleiner of gelijk aan g(x) . ik had -6 x x  2 2
jeroen
Leerling bovenbouw havo-vwo - dinsdag 20 juli 2010
Antwoord
Hallo,
Eigenlijk vervullen wij niet de functie van een uitwerkingboekje, maar aangezien je waarschijnlijk geen uitwerkingboekje van het tentamen hebt wil ik je de spanning van het wachten wel wegnemen.
Vraag 1
a) Goed antwoord
b) Gedeeltelijk goed, je heb slechts één van de twee antwoorden (kwadratisch verband). Hieronder mijn uitwerking, controleer wel of ik de vergelijking goed overgenomen heb...
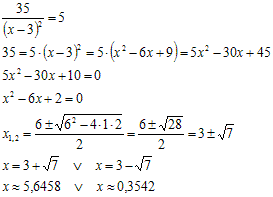
Vraag 2
a) Moeilijk te zeggen of je ze goed hebt. Controleer zelf even (controleer ook of ik de juiste formules heb gebruikt):
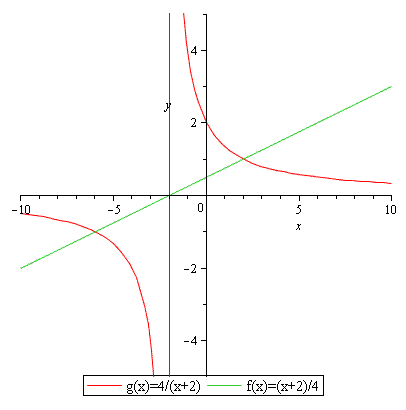
De rode verticale lijn is de verticale asymptoot van g(x)
b) Goed antwoord
c) De notatie is niet goed en roept ook verwarring op.
-6 x x 2 wil dus zeggen x 2 wil dus zeggen x -6 & x -6 & x 2. Hier klopt iets niet in: Als x 2. Hier klopt iets niet in: Als x -6, dan is geldt sowieso al dat x -6, dan is geldt sowieso al dat x 2. 2.
Als je nog eens goed naar de grafieken kijkt zie je het volgende:
Snijpunten: x=2 en x=-6 (zie vraag b)
Vanuit x=-6 gezien: Waar is f(x) (de groene) kleiner of gelijk? Dat is voor x=-6 en lager. Dus: x 6 6
Vanuit x=2 gezien: Waar is f(x) (de groene) kleiner of gelijk? Dat is voor x=2 en lager, maar...Komt de groene links van de rode verticale asymptoot (x=-2, dit is de waarde waarvoor g(x) niet bestaat) dan is f(x) weer in één keer groter dan g(x). Vanuit x=2 gezien geldt dus: -2 x x 2 2
Antwoord: x -6 & -2 -6 & -2 x x 2 2
Hopelijk heb ik je de antwoorden gegeven waar je op gehoopt had.
Mvg
Thijs Bouten

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 20 juli 2010
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 x
x  2
2
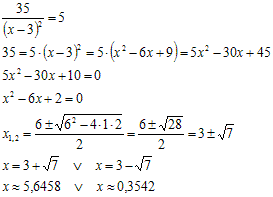

 x
x 2 wil dus zeggen x
2 wil dus zeggen x

 Re: Vergelijking
Re: Vergelijking