ik heb gisteren een tentamen gehad wil laten controleren of ik het goed heb gedaan.
vraag 1
a) Ö(x2-5)= 2. Ik heb als antwoord x= 3 of -3
b) 35/(x-3)2= 5. Ik heb als antwoord 5,6457. (Ö van 7 en dan + 3)
vraag 2
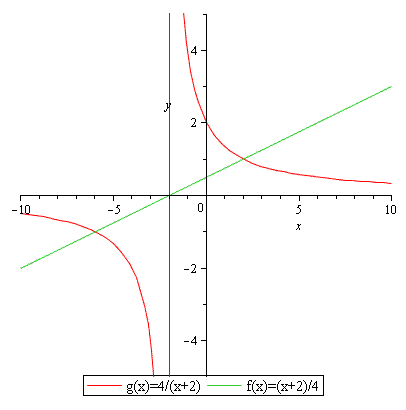
a) schets in 1 figuur de grafieken van de functies.
f(x)= x + 2/4 g(x)= 4/x+2
b) bereken alle snijpunten van de grafieken van f en g
ik had hier (-6,-1) en (2,1)
c)voor welke waarden van x is f(x) kleiner of gelijk aan g(x) . ik had -6
 x
x  2
2
jeroen
20-7-2010
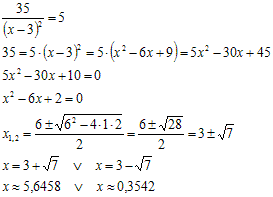
 x
x 2 wil dus zeggen x
2 wil dus zeggen x