|
|
|
\require{AMSmath}
Bereken en toon aan in een driehoek
Beste,
Volgende vraag krijg ik niet opgelost. Ik probeer dit te doen aan de hand van de sinusregel en cosinusregel maar raak er niet uit.
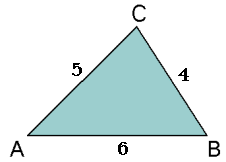
In de driehoek ABC:
a/4 = b/5 = c/6
met a = BC en b = AC en c = AB.
1. Toon aan dat hoek C = 2 keer hoek A
2. Bereken tan (hoek A/2)
Sam
3de graad ASO - donderdag 7 januari 2010
Antwoord
a.
Met de cosinuregel:
$
\begin{array}{l}
\left. \begin{array}{l}
4^2 = 5^2 + 6^2 - 2 \times 5 \times 6 \times \cos \alpha \Rightarrow \cos \alpha = \frac{3}{4}\,\,en\,\,\sin \alpha = \frac{1}{4}\sqrt 7 \\
6^2 = 4^2 + 5^2 - 2 \times 4 \times 5 \times \cos \gamma \Rightarrow \cos \gamma = \frac{1}{8}\,\,en\,\,\sin \gamma = \frac{3}{8}\sqrt 7 \\
\end{array} \right\} \Rightarrow \\
\sin (2\alpha ) = 2\,\sin \alpha \cos \alpha = 2\, \times \frac{1}{4}\sqrt 7 \times \frac{3}{4} = \frac{3}{8}\sqrt 7 = \sin \gamma \Rightarrow \gamma = 2\alpha \\
\end{array}
$
b.
$
\eqalign{\tan \left( {\frac{1}{2}\alpha } \right) = \frac{{\sin \alpha }}{{1 + \cos \alpha }} = \frac{{\frac{1}{4}\sqrt 7 }}{{1 + \frac{3}{4}}} = \frac{1}{7}\sqrt 7}
$
Zie eventueel Wikipedia | Lijst van goniometrische gelijkheden
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 9 januari 2010
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Re: Bereken en toon aan in een driehoek